
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:
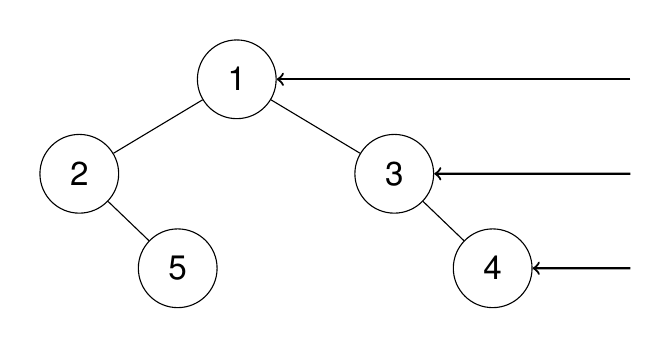
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
Example 2:
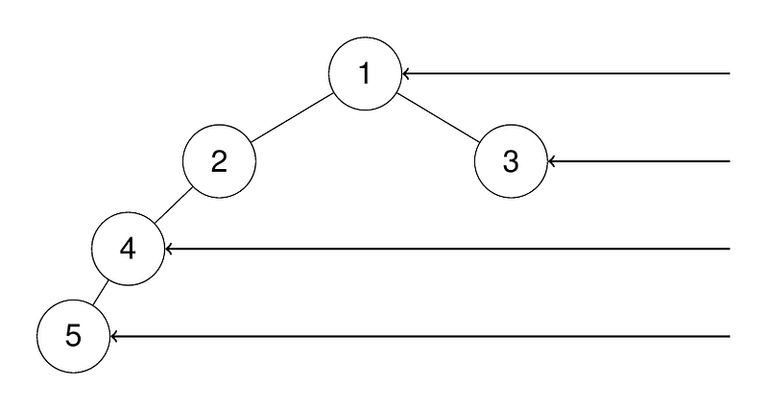
Input: root = [1,2,3,4,null,null,null,5]
Output: [1,3,4,5]
Example 3:
Input: root = [1,null,3]
Output: [1,3]
Example 4:
Input: root = []
Output: []
Constraints:
🚧The number of nodes in the tree is in the range [0, 100].
🚧-100 <= Node.val <= 100
🤓Explanation
Okay, imagine you're standing on the right side of a tree where each branch splits into two smaller branches (a binary tree). You can only see the nodes that are furthest to your right at each level of the tree. We want to find the values of these rightmost nodes, from top to bottom.
Imagine the tree has floors. On each floor, there might be one or two rooms. You are standing far to the right. You can only see the last room on each floor. We want to make a list of what's inside the last room you see on each floor, starting from the top floor.
function rightSideView(root):
# If the tree is empty, you see nothing.
if root is nothing:
return an empty list
# We'll use a line (queue) to keep track of the rooms on the current floor.
queue = put the root room in the line
# We'll make a list to remember what we see on the right side.
right_view = an empty list
# Keep going as long as there are rooms to look at.
while the line (queue) is not empty:
# Find out how many rooms are on the current floor.
number_of_rooms_on_this_floor = the number of rooms in the line
# Keep track of the last room we see on this floor.
last_room_seen = nothing
# Look at each room on this floor, from left to right.
for each room in the current floor (for each room in the line):
# Take the room out of the line.
current_room = take the first room out of the line
# This is the rightmost room we've seen so far on this floor.
last_room_seen = current_room
# If this room has a room to its left, put it in the line for the next floor.
if the current_room has a left room:
put the left room in the line
# If this room has a room to its right, put it in the line for the next floor.
if the current_room has a right room:
put the right room in the line
# After looking at all the rooms on this floor, the 'last_room_seen' is the one on the far right.
# Remember what's inside this rightmost room.
if last_room_seen is not nothing:
add the value inside last_room_seen to our 'right_view' list
# Finally, tell us what we saw on the right side, from top to bottom.
return the 'right_view' list
Implementations
🐍Python
# # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# from typing import Optional, List
from collections import deque
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
"""
Given the root of a binary tree, imagine yourself standing on the right side of it,
return the values of the nodes you can see ordered from top to bottom.
Args:
root: The root node of the binary tree.
Returns:
A list of integers representing the right side view of the binary tree.
"""
# If the tree is empty, there's no right side view.
if not root:
return []
# Initialize a deque to perform Breadth-First Search (BFS).
queue = deque([root])
# Initialize a list to store the nodes visible from the right side.
right_view = []
# Perform BFS level by level.
while queue:
# Get the number of nodes at the current level.
level_size = len(queue)
# Initialize a variable to keep track of the rightmost node at the current level.
rightmost_node = None
# Iterate through all the nodes at the current level.
for _ in range(level_size):
# Dequeue the current node.
node = queue.popleft()
# The last node processed at each level will be the rightmost node.
rightmost_node = node
# Enqueue the left child if it exists.
if node.left:
queue.append(node.left)
# Enqueue the right child if it exists.
if node.right:
queue.append(node.right)
# After processing all nodes at the current level, the rightmost_node
# is the one visible from the right side. Add its value to the result.
if rightmost_node:
right_view.append(rightmost_node.val)
# Return the list of nodes visible from the right side.
return right_view
🟦Typescript
/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
/**
* Given the root of a binary tree, imagine yourself standing on the right side of it,
* return the values of the nodes you can see ordered from top to bottom.
*
* @param {TreeNode | null} root The root node of the binary tree.
* @returns {number[]} A list of numbers representing the right side view of the binary tree.
*/
function rightSideView(root: TreeNode | null): number[] {
// If the tree is empty, there's no right side view.
if (!root) {
return [];
}
// Initialize a queue to perform Breadth-First Search (BFS).
const queue: (TreeNode | null)[] = [root];
// Initialize an array to store the nodes visible from the right side.
const rightView: number[] = [];
// Perform BFS level by level.
while (queue.length > 0) {
// Get the number of nodes at the current level.
const levelSize = queue.length;
// Initialize a variable to keep track of the rightmost node at the current level.
let rightmostNode: TreeNode | null = null;
// Iterate through all the nodes at the current level.
for (let i = 0; i < levelSize; i++) {
// Dequeue the current node.
const node = queue.shift();
// The last node processed at each level will be the rightmost node.
rightmostNode = node;
// Enqueue the left child if it exists.
if (node && node.left) {
queue.push(node.left);
}
// Enqueue the right child if it exists.
if (node && node.right) {
queue.push(node.right);
}
}
// After processing all nodes at the current level, the rightmostNode
// is the one visible from the right side. Add its value to the result.
if (rightmostNode) {
rightView.push(rightmostNode.val);
}
}
// Return the array of nodes visible from the right side.
return rightView;
};
🦀Rust
// // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None,
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
/// Given the root of a binary tree, imagine yourself standing on the right side of it,
/// return the values of the nodes you can see ordered from top to bottom.
///
/// # Arguments
///
/// * `root`: An optional `Rc<RefCell<TreeNode>>` representing the root node of the binary tree.
///
/// # Returns
///
/// A `Vec<i32>` containing the values of the nodes visible from the right side.
pub fn right_side_view(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
// If the tree is empty, there's no right side view.
if root.is_none() {
return Vec::new();
}
// Initialize a deque for Breadth-First Search (BFS).
let mut queue: VecDeque<Rc<RefCell<TreeNode>>> = VecDeque::new();
// Initialize a vector to store the nodes visible from the right side.
let mut right_view: Vec<i32> = Vec::new();
// Push the root node onto the queue.
queue.push_back(root.unwrap());
// Perform BFS level by level.
while !queue.is_empty() {
// Get the number of nodes at the current level.
let level_size = queue.len();
// Initialize a variable to keep track of the rightmost node at the current level.
let mut rightmost_node: Option<Rc<RefCell<TreeNode>>> = None;
// Iterate through all the nodes at the current level.
for _ in 0..level_size {
// Dequeue the current node.
if let Some(node_rc) = queue.pop_front() {
// Set the current node as the rightmost node encountered at this level.
rightmost_node = Some(node_rc.clone());
let node = node_rc.borrow();
// Enqueue the left child if it exists.
if let Some(left) = &node.left {
queue.push_back(left.clone());
}
// Enqueue the right child if it exists.
if let Some(right) = &node.right {
queue.push_back(right.clone());
}
}
}
// After processing all nodes at the current level, the rightmost_node
// is the one visible from the right side. Add its value to the result.
if let Some(node_rc) = rightmost_node {
right_view.push(node_rc.borrow().val);
}
}
// Return the vector of nodes visible from the right side.
right_view
}
}
If you liked this content I’d appreciate an upvote or a comment. That helps me improve the quality of my posts as well as getting to know more about you, my dear reader.
Muchas gracias!
Follow me for more content like this.
X | PeakD | Rumble | YouTube | Linked In | GitHub | PayPal.me | Medium
Down below you can find other ways to tip my work.
BankTransfer: "710969000019398639", // CLABE
BAT: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
ETH: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
BTC: "33xxUWU5kjcPk1Kr9ucn9tQXd2DbQ1b9tE",
ADA: "addr1q9l3y73e82hhwfr49eu0fkjw34w9s406wnln7rk9m4ky5fag8akgnwf3y4r2uzqf00rw0pvsucql0pqkzag5n450facq8vwr5e",
DOT: "1rRDzfMLPi88RixTeVc2beA5h2Q3z1K1Uk3kqqyej7nWPNf",
DOGE: "DRph8GEwGccvBWCe4wEQsWsTvQvsEH4QKH",
DAI: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875"