DSA (Medium) - Binary Tree - Maximum Level Sum of a Binary Tree (Python, Typescript & Go)

in #algorithms • 27 days ago


image.png

Given the root of a binary tree, the level of its root is 1, the level of its children is 2, and so on.

Return the smallest level x such that the sum of all the values of nodes at level x is maximal.

Example 1:


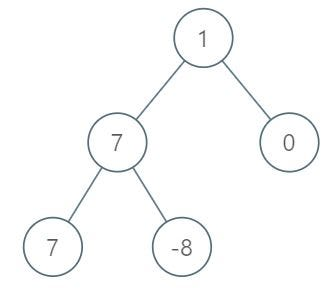
image.png

Input: root = [1,7,0,7,-8,null,null]
Output: 2
Explanation: 
Level 1 sum = 1.
Level 2 sum = 7 + 0 = 7.
Level 3 sum = 7 + -8 = -1.
So we return the level with the maximum sum which is level 2.

Example 2:

Input: root = [989,null,10250,98693,-89388,null,null,null,-32127]
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [1, 104].
  • -105 <= Node.val <= 105

🤓Explanation

Imagine you have a family tree, but it's organized in levels. The top person is level 1, their children are level 2, their grandchildren are level 3, and so on. Each person has a certain "value" associated with them (let's say, the number of cookies they baked).

The goal is to find out which level of the family baked the most cookies in total. If two levels baked the same highest number of cookies, we want the level that's closer to the top (smaller level number).

🍪Here's how we can figure this out, like a computer would:

  • Start at the very top of the tree (the 'root').
  • Keep track of levels, starting with level 1.
  • Keep a 'to-do' list of people to visit, initially just containing the root person.
  • Keep a record of the total cookies baked at each level, starting empty.
  • Now, do this repeatedly until the 'to-do' list is empty:

🍪 Look at everyone currently on the 'to-do' list. These are all the people at the current level.

  • Calculate the total cookies baked by everyone on this level.
  • Record this total for the current level.
  • Create a new 'to-do' list for the next level. This will contain all the children of the people on the current 'to-do' list.
  • Replace the old 'to-do' list with this new list of children.
  • Move to the next level (increase the level number by 1).

🍪Once we've gone through all the levels (the 'to-do' list is empty)

  • Look at our record of total cookies baked at each level.
  • Find the level that has the highest total.
  • If there's a tie for the highest total, pick the level with the smaller number (closer to the top).
  • Return this level number.

⚙️Implementations

🐍Python

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

from collections import deque
from typing import Optional

class Solution:
    def maxLevelSum(self, root: Optional[TreeNode]) -> int:
        """
        Finds the level with the maximum sum in a binary tree.
        If multiple levels have the same maximum sum, returns the smallest level index (1-based).

        Args:
            root: The root node of the binary tree (or None if the tree is empty).

        Returns:
            The 1-based index of the level with the maximum sum.
            Returns 0 if the tree is empty (though the problem statement implies a non-empty tree).
        """
        if not root:
            return 0  # Handle the case of an empty tree

        nodes_queue = deque([root])  # Initialize a queue for level-order traversal
        sums_per_level = []  # List to store the sum of nodes at each level

        while nodes_queue:
            level_sum = 0  # Initialize the sum for the current level

            # Calculate the sum of nodes at the current level
            # We iterate through all the nodes currently in the queue, which represent one level.
            for node in list(nodes_queue): # Iterate over a copy to avoid issues with modification
                level_sum += node.val

            sums_per_level.append(level_sum)  # Add the current level's sum to the list

            level_size = len(nodes_queue)  # Get the number of nodes at the current level

            # Process all nodes at the current level to add their children to the queue
            for _ in range(level_size):
                curr_node = nodes_queue.popleft()  # Dequeue the current node

                if curr_node.left:
                    nodes_queue.append(curr_node.left)  # Enqueue the left child if it exists

                if curr_node.right:
                    nodes_queue.append(curr_node.right)  # Enqueue the right child if it exists

        # Find the maximum sum among all levels
        max_sum = max(sums_per_level)

        # Find the index of the first occurrence of the maximum sum
        # The index in the list is 0-based, so we add 1 to get the 1-based level index.
        smallest_max_index = sums_per_level.index(max_sum)

        return smallest_max_index + 1  # Return the 1-based level index of the maximum sum

🟦Typescript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 * val: number
 * left: TreeNode | null
 * right: TreeNode | null
 * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 * this.val = (val===undefined ? 0 : val)
 * this.left = (left===undefined ? null : left)
 * this.right = (right===undefined ? null : right)
 * }
 * }
 */

/**
 * Given the root of a binary tree, return the level (1-indexed) with the largest sum.
 * If there are two or more levels with the same largest sum, return the smallest level index.
 *
 * @param {TreeNode | null} root The root of the binary tree.
 * @returns {number} The 1-indexed level with the largest sum. Returns 0 if the tree is empty.
 */
function maxLevelSum(root: TreeNode | null): number {
    if (!root) {
        return 0; // Handle the case of an empty tree
    }

    const queue: (TreeNode | null)[] = [root]; // Initialize a queue for level-order traversal
    let maxSum = -Infinity; // Initialize the maximum sum found so far
    let maxLevel = 0; // Initialize the level with the maximum sum
    let level = 1; // Initialize the current level number (1-based)

    while (queue.length > 0) {
        let levelSum = 0; // Initialize the sum for the current level
        const levelSize = queue.length; // Get the number of nodes at the current level

        // Iterate through all nodes at the current level
        for (let i = 0; i < levelSize; i++) {
            const currentNode = queue.shift(); // Dequeue the current node

            if (currentNode) {
                levelSum += currentNode.val; // Add the current node's value to the level sum

                // Enqueue the left child if it exists
                if (currentNode.left) {
                    queue.push(currentNode.left);
                }

                // Enqueue the right child if it exists
                if (currentNode.right) {
                    queue.push(currentNode.right);
                }
            }
        }

        // Check if the current level's sum is greater than the maximum sum found so far
        if (levelSum > maxSum) {
            maxSum = levelSum; // Update the maximum sum
            maxLevel = level; // Update the level with the maximum sum
        }

        level++; // Move to the next level
    }

    return maxLevel; // Return the 1-based index of the level with the maximum sum
}

🐭Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 * Val int
 * Left *TreeNode
 * Right *TreeNode
 * }
 */

import "math"

/**
 * Given the root of a binary tree, return the level (1-indexed) with the largest sum.
 * If there are two or more levels with the same largest sum, return the smallest level index.
 *
 * @param root *TreeNode The root of the binary tree.
 * @return int The 1-indexed level with the largest sum. Returns 0 if the tree is empty.
 */
func maxLevelSum(root *TreeNode) int {
 if root == nil {
  return 0
 }

 queue := []*TreeNode{root}
 maxSum := math.MinInt32 // Initialize maxSum to the smallest possible integer
 maxLevel := 0
 level := 1

 for len(queue) > 0 {
  levelSum := 0
  levelSize := len(queue)

  // Process all nodes at the current level
  for i := 0; i < levelSize; i++ {
   currentNode := queue[0]
   queue = queue[1:] // Dequeue

   if currentNode != nil {
    levelSum += currentNode.Val

    // Enqueue left child
    if currentNode.Left != nil {
     queue = append(queue, currentNode.Left)
    }

    // Enqueue right child
    if currentNode.Right != nil {
     queue = append(queue, currentNode.Right)
    }
   }
  }

  // Check if the current level's sum is greater than the maximum sum found so far
  if levelSum > maxSum {
   maxSum = levelSum
   maxLevel = level
  }

  level++
 }

 return maxLevel
}

If you liked this content I’d appreciate an upvote or a comment. That helps me improve the quality of my posts as well as getting to know more about you, my dear reader.

Muchas gracias!

Follow me for more content like this.

X | PeakD | Rumble | YouTube | Linked In | GitHub | PayPal.me | Medium

Down below you can find other ways to tip my work.

BankTransfer: "710969000019398639", // CLABE
BAT: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
ETH: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
BTC: "33xxUWU5kjcPk1Kr9ucn9tQXd2DbQ1b9tE",
ADA: "addr1q9l3y73e82hhwfr49eu0fkjw34w9s406wnln7rk9m4ky5fag8akgnwf3y4r2uzqf00rw0pvsucql0pqkzag5n450facq8vwr5e",
DOT: "1rRDzfMLPi88RixTeVc2beA5h2Q3z1K1Uk3kqqyej7nWPNf",
DOGE: "DRph8GEwGccvBWCe4wEQsWsTvQvsEH4QKH",
DAI: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875"
#dsa #softwareengineering #softwaredevelopment #python #javascript #go #golang #typescript #nodejs
27 days ago in #algorithms by
$0.00
    1 vote
    • and 1 more
    Reply 0
    Sort:  
  • Trending