之前学过一点 Python 知识,主要是要做数值计算,但是限于能力有限,也没有出什么结果, @etzel 在写Python 教学,我便抄打了一遍(写得特别详细),算是作业,也是练习。
主要内容:利用数值方法模拟出星球的轨道
用到的物理公式和数值方法可看 @etzel 的文章Python 繪製星球軌道教學(1)。
Python 的应用
numpy 是一个科学计算的包,包括强大的多维数组功能和许多数学方法。
matplotlib 是一个绘图包,类似于Matlab,语法上也基本相同。
numpy.linalg.norm() 是一个求范数的函数,一般用法是 numpy.linalg.norm(x, ord = None),
其中,
| 参数 | 说明 | 计算方法 |
|---|---|---|
| 无 | 二范数 |  |
| ord=2 | 二范数 | 同上 |
| ord=1 | 一范数 |  |
| ord=np.inf | 无穷范数 |  |
ggplot 是一个图的类型,很不错。
结果及代码
这里只是二维的图和代码,三维可看 @eztel 的文章。
运行输入参数:
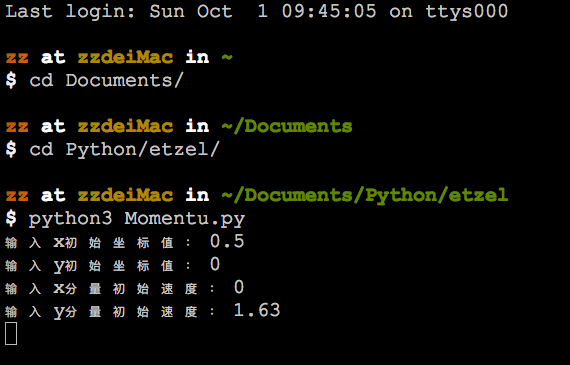
x = 0.5 y = 0 Vx = 0 Vy = 1.63
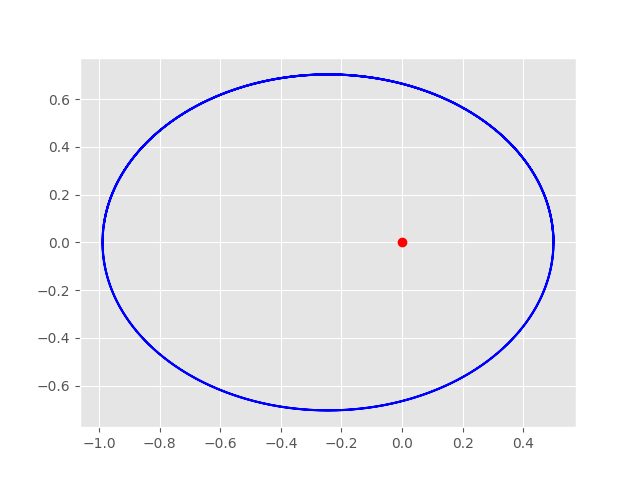
x = 0.5 y = 0 Vx = 0 Vy = 2
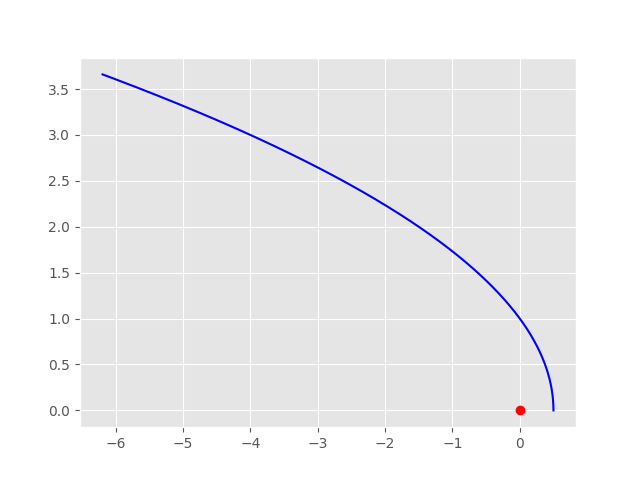
x = 0.5 y = 0 Vx = 0 Vy = 0.2
代码
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm
from matplotlib import style
style.use('ggplot')
fig = plt.figure()
Ax = fig.gca()
epsilon = 0.0001
n = 100000
position = np.zeros((n,2))
velocity = np.zeros((2))
acceleration = np.zeros((2))
position[0,0] = float(input("输入x初始坐标值:"))
position[0,1] = float(input("输入y初始坐标值:"))
velocity[0] = float(input("输入x分量初始速度:"))
velocity[1] = float(input("输入y分量初始速度:"))
r = norm(position[0])
r3 = 1/(r**3)
acceleration = position[0] * -r3
velocity += acceleration * epsilon * 0.5
i = 1
while(i<n):
position[i] = position[i-1]+velocity*epsilon
r = norm(position[i])
r3 = 1/(r**3)
acceleration = position[i]*-r3
velocity += acceleration*epsilon
i += 1
plt.plot(position[:,0], position[:,1],'b-')
plt.plot(0,0,"ro")
plt.show()
哇⊙ω⊙
比较基础,我还是抄的,哈哈
你要不要嘗試挑戰回答我文末的兩個問題呢?回答成功我就給你 2SBD!大家也可以來挑戰!
好强大
tvb姐学起来
我也要学!!
学起来~
嗯,我书都买完了哈哈哈
博士,写写教程
什么?我写教程吗?
别闹,这里用python的高手这么多。
写写呗,自己写自己的就好
我尝试写一写科技的。。