The Elements of Euclid - Part 1

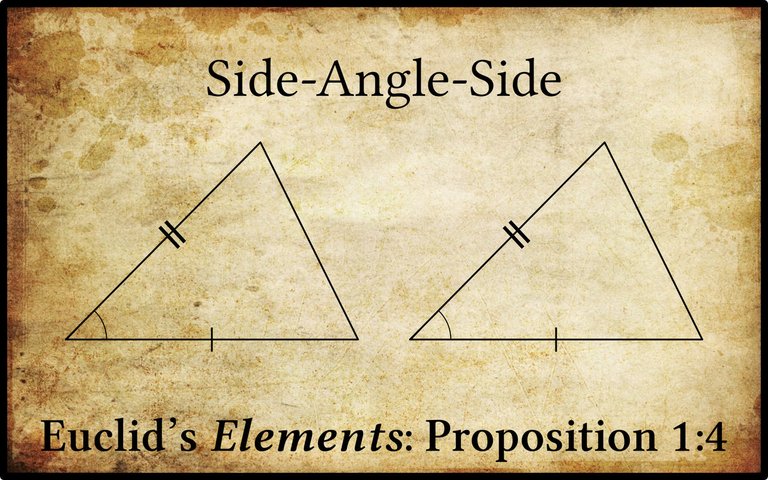
Book 1 of Euclid’s Elements opens with three constructions. The fourth proposition is the first true theorem.

This is the familiar Side-Angle-Side Theorem―also known as the SAS Theorem or SAS Congruence Theorem. Euclid’s wording is awkward and his demonstration of this proposition has been the subject of much criticism over the centuries. The proof requires one to apply one triangle to the other and to then show that, when thus superimposed, the applied triangle coincides perfectly with the other triangle. Common Notion 4 is then invoked to conclude that things coinciding with one another are equal to one another:

In the note on Common Notion 4 I have already mentioned that Euclid obviously used the method of superposition with reluctance, and I have given, after Veronese for the most part, the reason for holding that that method is not admissible as a theoretical means of proving equality, although it may be of use as a practical test, and may thus furnish an empirical basis on which to found a postulate. ―Heath 248–249

Dionysius Lardner

The Irish science writer Dionysius Lardner, who brought out a commentary on the first six books of the Elements in 1848, made the interesting point that in proving Proposition 1:4 Euclid does not use Common Notion 4 but rather its converse:

In the demonstration of this proposition, the converse of the eighth axiom [Lardner’s version of Common Notion 4] is assumed. The axiom states, that ‘if two magnitudes coincide they must be equal.’ In the proposition it is assumed, that if they be equal they must under certain circumstances coincide. ―Lardner 18

In modern terminology Euclid’s proof of this theorem is as follows:

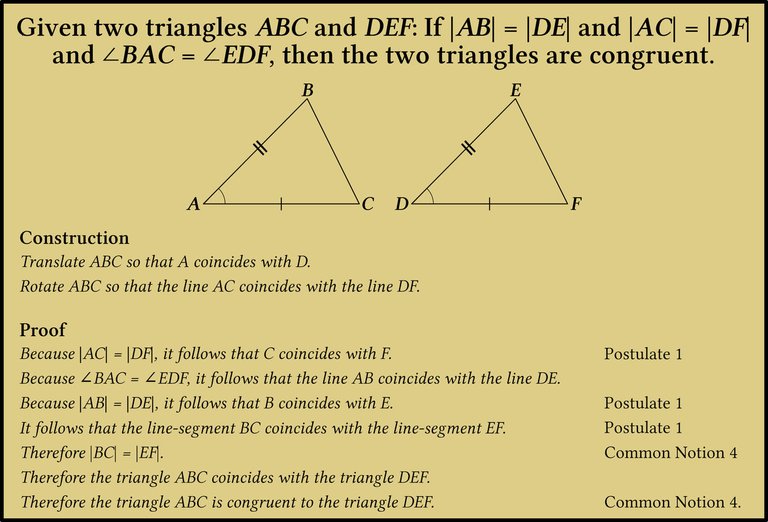
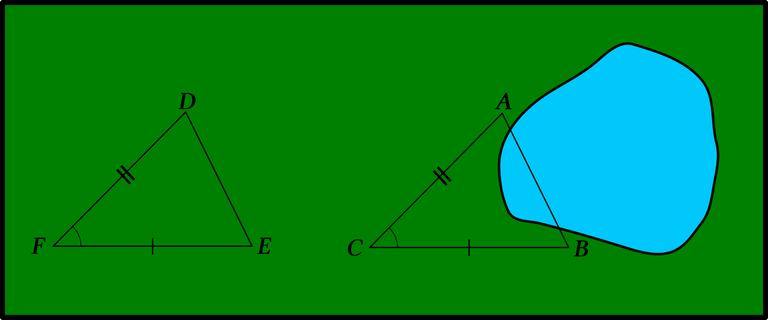
Euclid’s method of superposition, in which one triangle is applied to another, would be carried out by a modern geometer as a composition of two transformations: a translation followed by a rotation. As these transformations are isometries, they preserve length, area and measure of angle. Euclid, however, never defines any such transformations. He only uses the method of superposition three times in the Elements: 1:4, 1:8 and 3:24.

Another problem with Euclid’s proof is that it fails to take into account the possibility that the two triangles are mirror images of one another. The SAS Theorem applies to such figures, which are considered congruent. But the application of one of the triangles to the other now requires a composition of three isometries: a reflection in a line followed by a translation followed by a rotation. Reflecting one of the triangles in a line transforms it into its own mirror image, or enantiomorph.

Congruent Enantiomorphic Triangles

Thales

According to the Nigerian mathematician Michael C Dokai (see below), the SAS Theorem was known to the early Greek philosopher Thales of Miletus:

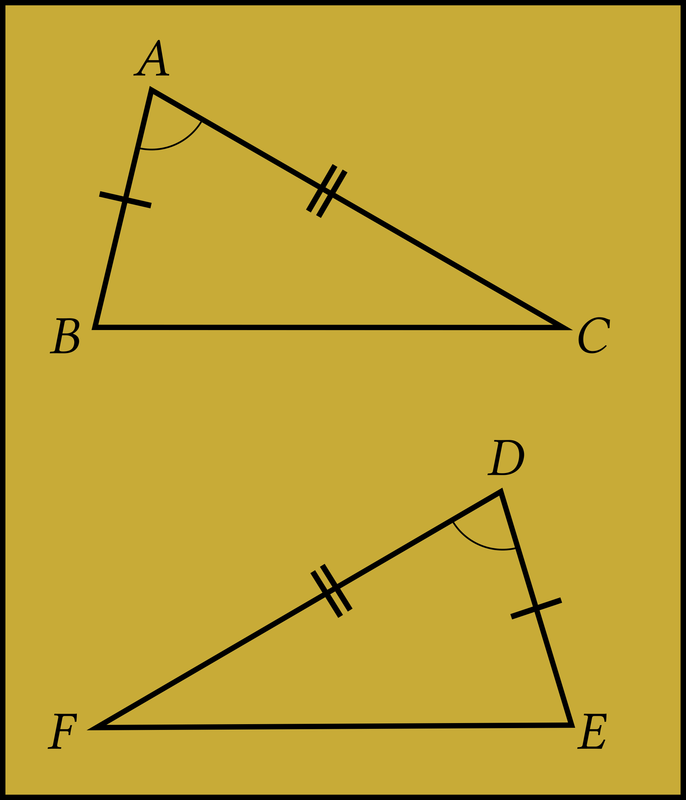
History has it that a great Greek geometer and wealthy merchant by the name of Thales of Miletus (Ca.640 to Ca.546BC) was asked to solve a surveying problem. He was asked to determine the distance between two points, A and B which were separated by a lake ...

In order to achieve this purpose, Thales took a third point C outside the lake from where he measured the distances CA and CB and, also, the angle ACB. Then he moved to a space outside the lake and constructed the triangle DEF such that FD = CA, FE = CB and angle DFE = angle ACB fig (ii). He then came to the conclusion that the triangles ABC, DEF were equal in all respects and therefore that AB = DE.

His conclusion followed from the fact that superimposing ∆DFE on ∆ABC would give exact fit of the two triangles. This method of using the equality of a pair of sides and the included angles to show that two triangles were congruent became known as SAS (side angle side). ―Dokai 26

Dokai cites no source for this anecdote and I have been unable to verify it. Five theorem are traditionally attributed to Thales. One of these relates to the congruence of triangles. According to a handful of sources I consulted this was the SAS Theorem, but most sources identify Thales’ congruence theorem as the Angle-Side-Angle or ASA Theorem (Euclid’s Proposition 1:26). Thales is alleged to have used ASA to determine the distance of ships at sea.

Bertrand Russell

The British philosopher and mathematician Bertrand Russell was not terribly impressed by this theorem. In an early paper entitled The Teaching of Euclid (1902) he wrote:

It has been customary when Euclid, considered as a text-book, is attacked for his verbosity or his obscurity or his pedantry, to defend him on the ground that his logical excellence is transcendent, and affords an invaluable training to the youthful powers of reasoning. This claim, however, vanishes on a close inspection. His definitions do not always define, his axioms are not always indemonstrable, his demonstrations require many axioms of which he is quite unconscious. A valid proof retains its demonstrative force when no figure is drawn, but very many of Euclid’s earlier proofs fail before this test ...

The fourth proposition is a tissue of nonsense. Superposition is a logically worthless device; for if our triangles are spatial, not material, there is a logical contradiction in the notion of moving them, while if they are material, they cannot be perfectly rigid, and when superposed they are certain to be slightly deformed from the shape they had before. What is presupposed, if anything analogous to Euclid’s proof is to be retained, is the following very complicated axiom: Given a triangle ABC and a straight line DE, there are two triangles, one on either side of DE, having their vertices at D, and one side along DE, and equal in all respects to the triangle ABC. (This axiom presupposes the definition of the two sides of a line, for which see below.) When the existence of a triangle thus equal in all respects to ABC is assured, we can prove that the triangle considered in the fourth proposition is this triangle. Russell 1902:165–166

Bertrand Russell

The following year Russell elaborated on this criticism in The Principles of Mathematics:

390. The fourth proposition is the first in which Euclid employs the method of superposition―a method which, since he will make any détour to avoid it, he evidently dislikes, and rightly, since it has no logical validity, and strikes every intelligent child as a juggle. In the first place, to speak of motion implies that our triangles are not spatial, but material. For a point of space is a position, and can no more change its position than the leopard can change his spots. The motion of a point of space is a phantom directly contradictory to the law of identity: it is the supposition that a given point can be now one point and now another. Hence motion, in the ordinary sense, is only possible to matter, not to space. But in this case superposition proves no geometrical property. Suppose that the triangle ABC is by the window, and the side AB consists of the column of mercury in a thermometer; suppose also that DEF is by the fire. Let us apply ABC to DEF as Euclid directs, and let AB just cover DE. Then we are to conclude that ABC and DEF, before the motion, were equal in all respects. But if we had brought DEF to ABC no such result would have followed. But how foolish! I shall be told: of course ABC and DEF are to be both rigid bodies. Well and good. But two little difficulties remain. In the first place―and for my opponent, who is an empirical philosopher, this point is serious―it is as certain as anything can be that there are no rigid bodies in the universe. In the second place―and if my opponent were not an empiricist, he would find this objection far more fatal―the meaning of rigidity presupposes a purely spatial metrical equality, logically independent of matter. For what is meant by a rigid body? It is one which, throughout a continuous portion of time, preserves all its metrical properties unchanged. Hence we incur a most fatally vicious circle if we attempt to define metrical properties by rigidity. If αβγ be a material triangle, which occupies at one time the space ABC, at another the space AʹBʹCʹ, to say that αβγ is rigid means that, however the two times be chosen (within some assigned period), the triangles ABC, AʹBʹCʹ are equal in all respects. If we are to avoid this conclusion, we must define rigidity in some wholly non-geometrical manner. We may say, for example, that a rigid body means one which is made of steel, or of brass. But then it becomes a logical error to regard brass eternal as slave to mortal rage; and if we define equal spaces as those which can be occupied by one and the same rigid body, the propositions of metrical Geometry will be one and all false.

The fact is that motion, as the word is used by geometers, has a meaning entirely different from that which it has in daily life, just as a variable, in mathematics, is not something which changes, but is usually, on the contrary, something incapable of change. So it is with motion. Motion is a certain class of one-one relations, each of which has every point of space for its extension, and each of which has a converse also belonging to the class. That is, a motion is a one-one relation, in which the referent and the relatum are both points, and in which every point may appear as referent and again as relatum. A motion is not this only: on the contrary, it has this further characteristic, that the metrical properties of any class of referents are identical with those of the corresponding class of relata. This characteristic, together with the other, defines a motion as used in Geometry, or rather, it defines a motion or a reflexion; but this point need not be elucidated at present. What is clear is, that a motion presupposes the existence, in different parts of space, of figures having the same metrical properties, and cannot be used to define those properties. And it is this sense of the word motion, not the usual material sense, which is relevant to Euclid’s use of superposition.

391. Returning now to Euclid’s fourth proposition, we see that the superposition of ABC on DEF involves the following assumptions. (1) On the line DE there is a point E, on either side of D, such that DE = AB, This is provided for by the postulate about the circle. (2) On either side of the ray DE, there is a ray DF such that the angle EDF is equal to the angle BAC. This is required for the possibility of a triangle DEF such as the enunciation demands, but no axiom from which this follows can be found in Euclid. The problem, to construct an angle EDF equal to BAC, does not occur till I.23, and there I.4 is used in the proof. Hence the present assumption must be added to Euclid’s axioms. It now follows that on DF there is a point F such that DF = AC. Hence the possibility of two such triangles as the enunciation demands is established. But in order to prove that DEF is equal in all respects to ABC, we need a further axiom, namely: With one angle at D, one side along the ray DE, and the other side to the right (or left) of DE, there exists a triangle which is equal in all respects to the triangle ABC. This is, in fact, the exact assumption which is concealed in the method of superposition. With this assumption, it finally becomes possible to prove that DEF is the triangle satisfying the above conditions and equal in all respects to ABC. ―Russell 1903:405–407

David Hilbert

The German geometrist David Hilbert avoided all these difficulties by essentially assuming Proposition 1:4 as an axiom. In his Grundlagen der Geometrie [Foundations of Geometry] the Side-Angle-Side Theorem is Hilbert’s Theorem 10, but the proof of this theorem follows directly from Axiom IV:6, Axiom IV:5 and Axiom IV:4, as we read in Edgar Jerome Townsend’s English translation. Note that I have corrected a typo in line 9 of page 18 of Hilbert & Townsend:

Hilbert & Townsend 17–18

Proving the SAS Theorem

In 2014 the Nigerian mathematician Michael C Dokai offered what he claimed was the first analytic proof of the SAS Theorem:

The aim of this research is to find a proof of the elusive side angle side (SAS) theorem of Euclid on the congruence of triangles using the cross section of a double cone. It is known that the SAS theorem has remained analytically unproved for over 2000 years. The method used for over 2000 years for proving this very important side angle side (SAS) theorem of Euclid has been the method of superposition whereby two triangles are tested for congruence by applying one to the other. ―Dokai 26

Dokai’s proof, however, relies upon what he calls the Axiom of Movement:

... an axiom long laid down by the Greeks. It is the axiom of movement of geometric figures.

Axiom: Any geometric figure may be moved from one place to another without changing its size or shape. ―Dokai 27

Dokai’s proof, then, is open to the same criticisms Russell levelled at Euclid’s proof. It appears that the proofs of congruence theorems must begin with at least one such theorem being taken as axiomatic and using it as a foundation on which to base the proofs of the others.

And that’s a good place to stop.

---

References

• Michael C Dokai, A Proof of Euclid’s SAS (Side Angle Side) Theorem of Congruence of Triangles via the Cross Section of a Double Cone, IOSR Journal of Mathematics, Volume 10, Issue 1, Pages 26–33, IOSR, Ahmedabad, Gujarat, India (2014)
• Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
• Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
• David Hilbert, E J Townsend (translator), Foundations of Geometry, Second Edition, The Open Court Publishing Company, Chicago (1910)
• Dionysius Lardner, The First Six Books of the Elements of Euclid, Eleventh Edition, Henry G Bohn, London (1855)
• Bertrand Russell, The Teaching of Euclid, The Mathematical Gazette, Volume 2, Number 33, Pages 165–167, George Bell & Sons, London (1902)
• Bertrand Russell, The Principles of Mathematics, Cambridge University Press, Cambridge (1903)

Image Credits

• Bertrand Russell: London Stereoscopic & Photographic Company, Public Domain
• Dionysius Lardner: Thomas Bridgford (original artist), National Portrait Gallery, London, Public Domain

Online Resources

• Euclid’s Elements by David E Joyce
• Life of Euclid
• Reading Euclid