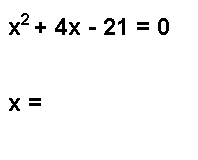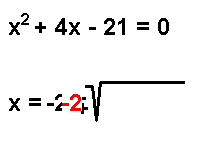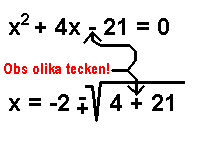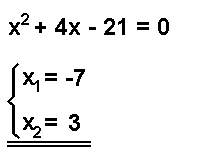
Okay. Let's get started. The first person to solve the word problem below will get an upvote worth $0.7. There will also be some consolation upvotes for some of the late comers.
How To Participate:
Kindly UPVOTE this post and then answer the question which follows in the comment section. Entries that do not comply with this simple rule will be disregarded.
Question:
The minute hand of a wall clock is 14cm long. Given that the time is 11am, calculate the distance travelled by the minute hand when the time is exactly 11:15 am.
Deadline:
The test comes to an end once a winner emerges or at the expiration of this post. Good luck guys.
Thanks for visiting this channel @steemitcentral. Use the "steemitcentral" tag in your Steemit or crypto-related posts and get rewarded with some upvotes.

Well I would use the formula C=(1/4)pidiameter to get the distance traveled by the minute hand.
So it would look like C=(1/4)pi28
This would make the answer 7*pi or about 21.991 cm
Congratulations! YOU WON.
Great job :)
HELLO
ACCORDING TO MY MEASUREMENTS AND CALCULATIONS THE ANSWER SHOULD BE 20 CENTIMETERS.
Very close, but could be a bit better :) how did you do it?
did you say the minute hand has 14 cm. long
so i place the clock at 11:00 then i rotate the minute hand thru 11:15 and i took measurement from one point to another and my result was 20 cm.
so if a was wrong i hope someone can do it better.
thanks
ah I see it was close so i got curious :) it should be 22 if calculated!
Thanks!
X=3
It is the question in text below, how long the minute marker moves in CM during 15 min, if the minute marker it self is 14 cm.
13 centimeters?
Not quiet :) take another guess!
Will someone get the correct answer? :O
Hahaha I hope someone does.
14cm
Not quiet
The answer is 21.98cm...which is approximately 22cm
The minute hand serve has a radius. It moves 11am to 11:15 which is 90degrees. Using radian×radius. A radian is 180degrees which is equivalent to a pie(3.14). But here it moved 90degrees, which is 3.14/2=1.57..so the distance covered is 1.57×14=21.98
Nice, you get second place, a bit late :)
Answer is 44cm
Actually, it depends on how you define the "distance traveled" I would argue the distance traveled by the minute handle is 90° or pi/2 rad.
The distance traveled by the tip of the minute handle is pi/2 times 14 cm, i. e. (as stated before) 7pi or about 21.991 cm.
Equally unambiguous would be the area swept by the minute handle (assuming it doesn't have a tail). Which would be equal to pi times 14 squared divided by 4, or 49 pi being about 153.938 square cm.