
The concept of function is the fundamental basis in infinitesimal calculus, that is why I want to explain the concept of function, function notations and other concepts such as domain and range of a real function.
Definition of real function of a real variable
Let X and Y be a set of real numbers. A real function f of a real variable x from X to Y is a correspondence that assigns to each number x of X exactly one number of y of Y.
The domain of f is the set X. The number y is the image of x by f and is denoted by f(x), which is called the value of f at x. The path or range of f is defined as the subset of Y formed by all the images of the numbers of X.
All this is explained in the following figure:

Functions can be expressed in multiple ways. However, in this case I only want to explain functions with dependent and independent variables, such as:
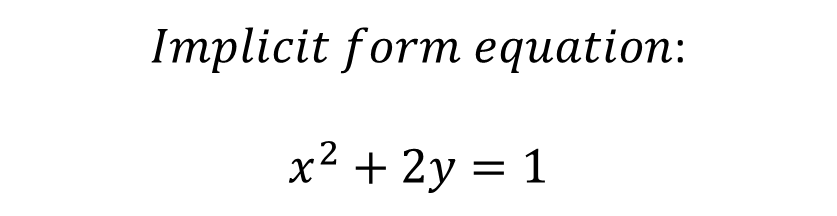
To express in function form, it is convenient to clear y:
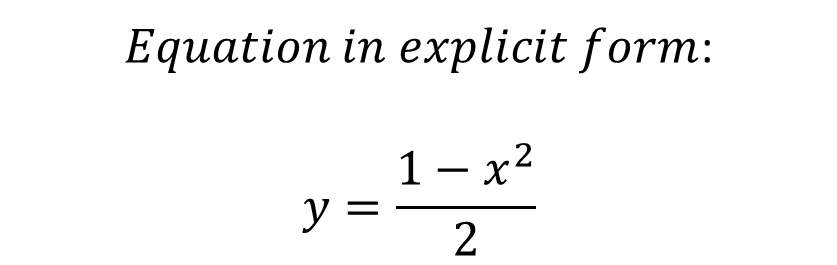
If we use f as the name of the function, then this equation can be written:
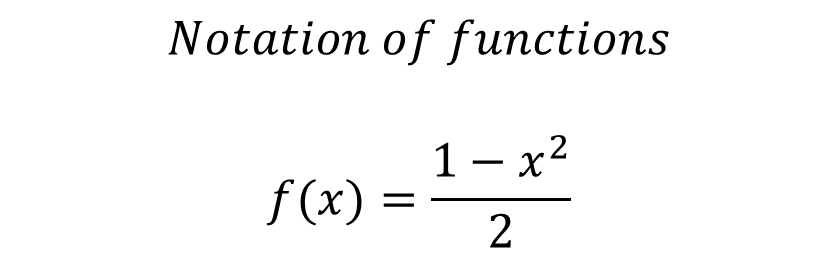
Depending on how a function is denoted or expressed, it is possible to have the advantage of being able to identify the dependent variable as follows f(x), and at the same time we can express that the independent variable is x and that the function is denoted by "f".
The symbol f(x) se lee “f of x”. Function notation has the advantage of saving words, since instead of asking:
What is the value of y corresponding to x=3?
You can ask in a more summarized form:
What is the value of f(3)?
We could then state that if we have an equation that defines a function, then the role of the variable x is simply that of a gap to be filled. For example, the function given by:
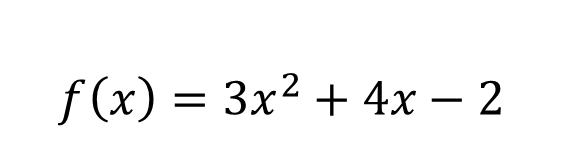
Which can be described as:
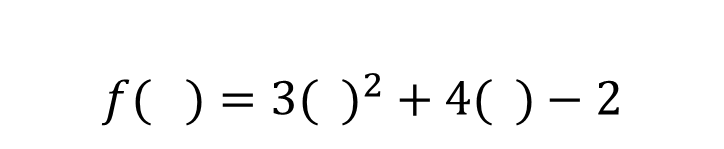
To evaluate such a function considering that we can substitute any real number inside the parenthesis, for example for x = 2, implies that:

It is important to note that although it is very common to use f as a suitable symbol to denote a function and x for the independent variable, it should be noted that other symbols can be used without any problem. For example, all of the following equations represent the same function:
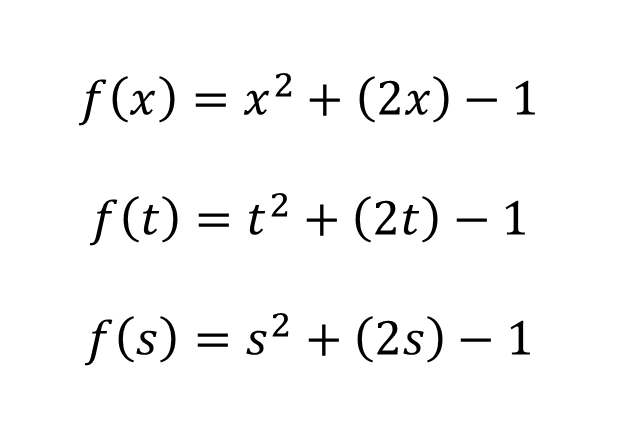
The function is the same, what changes is the independent variable, which for the first case is x, for the second case is t and for the third case is s.
Bibliographic Reference
Calculus with Analytic Geometry by Ron Larson, Robert, P. Hostetler and Bruce H. Edwards. Volume I. Eighth Edition. McGraw Hill. Año 2006