As someone who has recently dived deep into optimization and modeling, I have been experimenting with various ways of dealing with complex optimization problems. In this blog post, I will introduce the concept of linear programming and give a simple understanding of how to solve a linear programming problem using R. In fact, I want to share this with people who might be interested and also use this blog as a notebook.
 Decision Making by Nick Youngson
Decision Making by Nick YoungsonAlrighty, let me break it down for ya! So, basically, linear programming is a fancy-schmancy math technique used to optimize a linear objective function. In other words, it helps you find the best solution to a problem while making sure that a set of linear constraints are met. And let me tell ya, it's not just used in one field - no siree! You can find it being used all over the place, from finance to engineering to supply chain management.
Now, let me give you a reallife example of how linear programming can be used. I will keep it simple and use a lego problem. Yep, it's gonna be a blast! But first, we need to setting up the model. This is where we define the problem we're trying to solve, the objective we want to achieve, and the constraints we have to follow. And once we have all that set up, we can use a handy-dandy R package to find the optimal solution.
I gotta say, I've tried this out before and it's actually pretty fun. It's like solving a puzzle, but with math! So if you're into that sorta thing, I definitely recommend giving linear programming a try.
Suppose a furniture manufacturer is undecided about producing chairs and tables. Tables sell for 1600 dollars and chairs sell for 1000 dollars. The furniture maker has two different parts, small and large. The chair is made from 2 small and one large piece, while the table is made from 2 small and 2 large pieces. What decision should the manufacturer make to maximize profit?
In fact, we can represent this problem mathematically using a linear programming model. Here we will have an objective function and some constraints. Our objective is to maximize the revenue from the number of tables and chairs to be produced, but on the other hand there is a limited number of materials. So we will need to write constraint functions and look for an optimization method in this way.
Let's take a look at the model below:
Maximize: 1600x1 + 1000x2
Subject to: 2x1 + x2 <= 6
2x1 + 2x2 <= 8
x1, x2 >= 0
Initially, we can define the number of tables and chairs to be produced as x1 and x2 respectively. With our objective function we want to maximize the total revenue in a linear combination. On the one hand, we will need equations to represent the number of large and small pieces. The last but not less important constraint is that these variables can never be negative.
Now, let's move on to solving this linear programming problem using R. I will use lpSolve, a popular package for linear programming in R.
# Objective function
library(lpSolve)
#defining parameters
obj.fun.p <- c(1600, 1000)
constr <- matrix(c(2,1,
2,2), ncol = 2, byrow = TRUE)
rhs <- c(6, 8)
constr.dir <- c("<=", "<=")
#solving model
prod.sol <- lp("max", obj.fun.p, constr, constr.dir, rhs, compute.sens = TRUE)
#accessing to R output
prod.sol$objval #Obj fun. value
prod.sol$solution #decision variable values
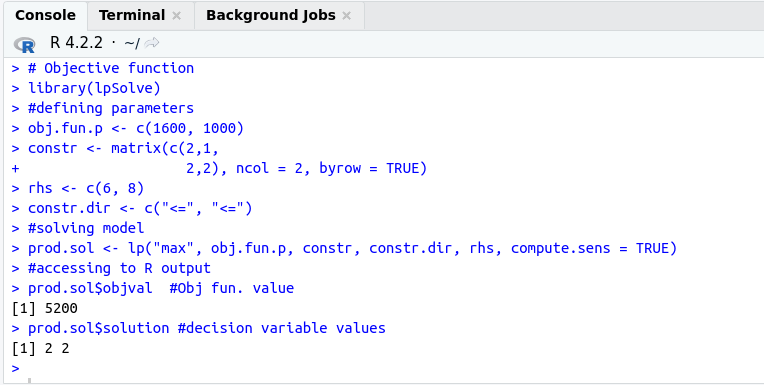
The R package is really a great benefit. As a result, we found the optimum plan to be 2 tables and 2 chairs, which means a total income of 5200 dollars. With the geometric solution below, we can actually capture how we can easily achieve this.
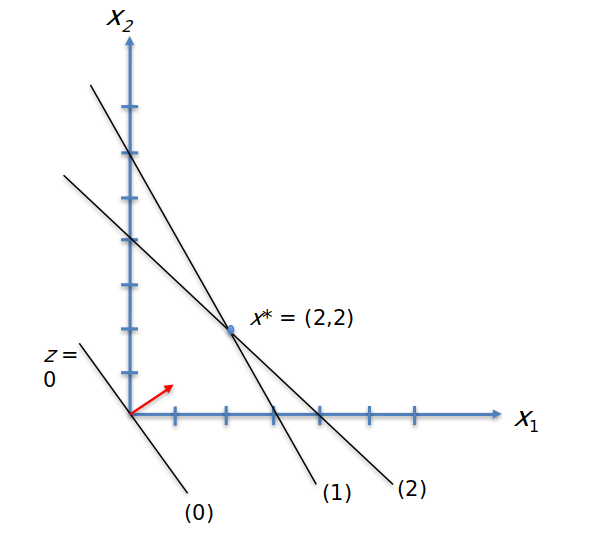
Let me remind you that linear programming is a powerful mathematical technique that allows us to optimize a linear objective function subject to linear constraints, and it has many different variants. When I have time, I would like to revisit these variants with different problems. In addition to finding them with R packages, I think it is very important to look at the different techniques to understand the logic. Looking at the geometric solution and others...
Keep learning and optimizing!
Posted with STEMGeeks
Optimizing Furniture Production with Linear Programming (LP) involves employing mathematical techniques to streamline manufacturing processes and maximize efficiency. By leveraging LP, furniture manufacturers can minimize costs, optimize material usage, and improve production timelines. One key element in this optimization is the implementation of high-quality hardware like the hinge system from https://www.keahardware.com/product/hinge-system. Integrating such reliable components enhances the overall durability and functionality of furniture, ensuring customer satisfaction and long-term success in the industry.