It's been some time since the last post! I'm actually still doing Leetcode from time to time, and I have a friend who just started learning algorithms a few days ago so we did quite a bunch of questions together as well. However, not all questions are good post-writing materials, and life always throw things at you when you least expect it. Ahem. Anyways, let's get to what we're looking at today...
At the end of the first page of the questions listing on Leetcode, on number 50, there's this question, Pow(x, n). If you click into it, you'll see that it has a somewhat interesting like to dislike ratio, basically saying that the part of the community that doesn't like this question is larger than the part that is happy with this question. This doesn't happen often, but when it happens, it generally means that the problem either has terrible test cases, or is too easy to cheat. Not entirely clear what is wrong about this question (I'm betting that it's the second case...), but hey, a question is a question. Let's get solving!
The requirement is really simple: It wants a function to calculate the result of x raised to the nth power. Pretty easy. I guess a lot of programming courses had gave exercises related to this to their students, especially on the lessons related to loops or recursion. Or, at least, throughout the courses I had taken, this question appeared at least twice...
For the last few times of me meeting a question like this, I solved it this way: Start from an answer value of 1, and start multiplying the number x onto it for a total of n times, then return the result. Or, divide the answer value by the number x for total of n times, if n is negative. Converting it into C# code, it's pretty much just 4 lines:
public class Solution {
public double MyPow(double x, int n) {
double res = 1;
if (n > 0) for (int i = 0; i < n; i++) res *= x;
else for (int i = 0; i > n; i--) res /= x;
return res;
}
}
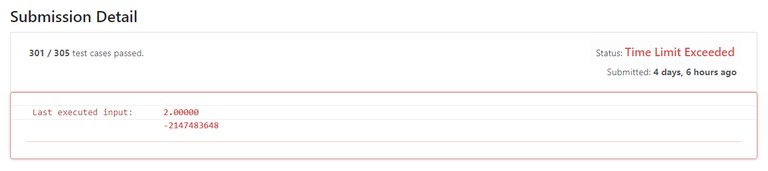
There is absolutely nothing that can go wrong with this. I mean, logically speaking, this implementation is absolutely correct. For it to fail, Leetcode must need to have some extremely broken test case that only the evilest QA member can think about. So, let's submit it...
...
bonk.
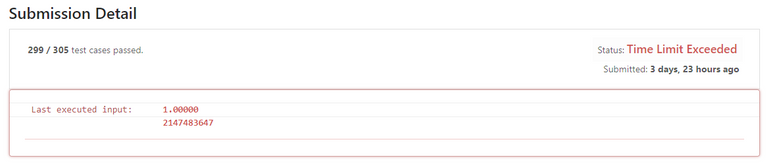

Okay... I forgot that execution time is another thing. Adding special case handling for when x = 1 does not work too, because the person adding the test case was smarter than us:
So, what do we do? You can't reasonably optimize the loop so much that it runs several times faster. There has to be another way, and there indeed is...
If you think of it, the calculation for raising numbers to a power can be split into several smaller similar calculations. For example, Pow(2, 8) can be split into two runs of Pow(2, 4), and Pow(2, 5) can be split into two runs of Pow(2, 2) and one more run of Pow(2, 1). Intuitively, this calls for a recursive function, and the code could look like this:
public class Solution {
public double MyPow(double x, int n) {
if (n == 1) return x;
if (n == 0) return 1;
if (n == -1) return 1/x;
return MyPow(x, n/2) * MyPow(x, n/2) * MyPow(x, n%2);
}
}
But this code did negative optimisations, since the total number of multiplications done would be more than the previous one! Take for the example of Pow(2, 8), it will first be split into two calls of Pow(2, 4) and one call of Pow(2, 0), then it will be further split... and in the end, we will get a total of 8 calls of Pow(2, 1) and probably... 7 calls of Pow(2, 0). That sounds much, much slower than the previous one, and in fact, it is - not only because it performs more multiplications, but also because it uses recursion. We all know that as much as recursion is cool, it runs slower than loops due to function call overhead. Hence, this code also passes lesser test cases than the previous one, dying at the 292th before getting to see the rest.
But, we're mostly on the right track. Although Pow(2, 8) is indeed two runs of Pow(2, 4) multiplied together, we don't need to calculate Pow(2, 4) twice - we can just save the result somewhere and reuse it. We also don't need to perform the third Pow() call, since it can only be either 1 or x, depending on if the n is even or not. That could have chopped the number of function calls required to calculate Pow(2, 8) all the way down to 4, as we only need to calculate Pow(2, 1), Pow(2, 2), Pow(2, 4) before we can get Pow(2, 8)!
And of course, liberally sprinkle bitwise operations here and there as you desire... because, uh, I don't know, it's a side effect of learning Assembly language? You'll have a special feeling against divide and modulo functions after learning about them in Assembly, especially when you are thinking too hard about performance. So here's what we have now.
public class Solution {
public double MyPow(double x, int n) {
if (n == 1) return x;
if (n == 0) return 1;
if (n == -1) return 1/x;
double tempRes = MyPow(x, n >> 1);
return tempRes * tempRes * ((n & 1) == 0 ? 1 : x);
}
}
If you have never heard about bitwise operations and some of these symbols are starting to look alien to you, here's what they mean: >> is an arithmetic right shift operation, which also brings the effect of dividing if you know what to do with it. Right shifting by 1 has the effect of dividing by 2, so it is used in place of it. The & is a logical AND operator, which... I think the link can do a better job than me in explaining what it is. So, click into the links if you need to know more!
By doing & 1 on a number, we can know if the number is even or odd, as the least significant bit of an odd number is always 1, and the least significant bit of an even number is always zero. This also applies to negative numbers. Hence, if n & 1 results in something that is not zero, we can know that n is an odd number, and we should multiply the result by x for one more time. ((n & 1) == 0 ? 1 : x) is a statement that uses the ternary conditional operator of C#, in which, if n & 1 is equal to 0, will return a value of 1, or x otherwise.
Hence, with the code above, Pow(2, 8) would be turned into Pow(2, 4) * Pow(2, 4) * 1, while Pow(2, 7) would be turned into Pow(2, 3) * Pow(2, 3) * 2. Sounds perfectly correct. But, how about negative numbers? Isn't it that right shifting negative numbers to divide them isn't correct all the time?

Indeed, if you have learnt about 2s complement, you might have noticed that right shifting negative numbers to divide them has some issues - but, although totally unplanned, our code happens to handle it right. Here's what is happening:
The thing about right shifting negative numbers to divide them is that they are correct for half of the time. If you right shift a negative even number, it'll be correct, for example, -4 (1111...1100 in binary) after right shifting by 1 will be 1111...1110, which is equals to -2. Right shifting a negative odd number however will cause the result to be smaller by the expected result by 1. For example, right shifting -3 (1111...1101) will result in 1111...1110, which is -2, while the expected result should be -1. The "correct way" to solve it happens to be just adding the number by 1 before shifting it. So, -4 will be incremented to -3, and after shifting we will get -2. On the other hand, -3 will be incremented to -2, and after shifting we will get -1. But, we didn't do that in our code!
However, remember the last part of our code where we multiply the thing by x if x is an odd number? It happens to handle the situation nicely - Let's say we have a situation of Pow(2, -3), we will get Pow(2, -2) * Pow(2, -2) * 2. Which, happens to still be correct (-2 + -2 + 1 = -3). If we chose to do the right shifting in the "correct" way for negative numbers, we would need another condition in the last part to return -x instead of x in the case of negative numbers.
It's a pleasant surprise finding, because we know that more if-conditions mean potentially (significantly) less performance! Now with this, it should work, right?
And it did.

After implementing the whole thing, I learned that there's something called
Binary Exponentiation, which, is pretty much what this algorithm is about. Well, implementing the solution myself still gives a special satisfaction, so it's good at the end. The link also contains an algorithm that doesn't use recursion (so it should be faster), so check it out if you are interested!
So, while scrolling through the discussion section of the problem on Leetcode, I found a few interesting things... mainly, you can "cheat" this problem if you try, and there are more than one way to do it.
First of all, very obviously, there is nothing stopping you from using functions or methods from standard math libraries, nor there is nothing stopping you from using raise-to-power operators that are available in languages like Python. So, you could do something like this for C#, and the system would gladly accept it. This solution might even be the fastest one possible...
public class Solution {
public double MyPow(double x, int n) {
return Math.Pow(x, n);
}
}
That naturally makes the problem quite disappointing to solve, because after all, if all you want is just the green "Accepted" text, you can just throw this in and it accepts it. Some other problems that stated that you should do this with O(1) memory also suffers from a similar issue where you can allocate a new array with size of the input and do stuff with it, and the system won't stop you with a memory limit exceeded error. Typically, problems like these don't get loved that much, even though it's still pretty fun to solve them in the "proper" way. Why? Maybe because people like to play fair, and the system accepting these solutions is not stopping others from breaking the rules and submitting their "illegal" solution to pollute the leaderboard. Guess that's a problem for Leetcode... I'm there for the fun, not for the %. :)
Oh, I came across this solution in the discussions board as well. It is, interesting, to say the least. Turns out that, if you try, and you know the limits of the input range, you can make some pretty daring "edge case handling" and clear the problem your own way. Maybe someone after seeing this solution will add a few more test cases to break it in the future...
And that's a lot for raising a number to a power! Thanks for reading it all the way till here. See you next time.
:)