Algorithms (aka "the word programmers use to explain things they don't want to go into details") is something I frequently deal with, due to my nerdy nature. Or maybe, my interest in software developing, as algorithms are pretty much the stuff responsible for a lot of magic happening behind applications. I enjoy tinkering around them, and it's always fun to learn new approaches to problems as people figure out faster and better ways to tackle them. Fascinating stuff. Of course it can also go the other way round with people developing hilariously terrible methods against certain problems, but it's still fascinating regardless. That's not the main point today, though.
(or is it...?)

A few days ago, my project manager sent us an algorithm-related programming question as a fun challenge.
Given an array of strings (e.g. { "happy", "hair", "hat" }), how to find the longest common prefix for those strings (e.g. "ha" from the array of strings above)?
It's not the exact question, but the requirement is the same: an algorithm that when given an array of strings, capable of finding the longest common prefix from them.
At first sight, this question reminded me of the Longest Common Subsequence problem, mainly because that prefixes are indeed considered in the set of subsequences, as subsequences are basically just strings you can form from the characters of a given string without reordering them (see the Wikipedia article for a more accurate explanation on them). The Longest Common Subsequence problem is pretty famous, and it's like a favourite question among algorithm teachers and probably interviewers, perhaps due to the simplicity of the question and the tricky algorithm to solve it optimally. So, I also know this question, but whether I can solve it without Google is another story.
...and the answer is of course no! I never really remembered the algorithm for that. However, I do know that the optimal approach uses dynamic programming, and I remember that the algorithm uses something like a table, and that's all I remember. The solution indeed uses those two stuff, though. Maybe I will need a revision on this problem some day when I really need to use it practically, but anyway, back to topic...
Indeed, at first sight on this longest common prefix problem, I immediately thought about the solution for the Longest Common Subsequence problem and went, "well, so we need dynamic programming for this? I don't like that". But it very quickly dawned on me that we are only looking for the longest prefix, which is honestly, pretty trivial to find.
In human language, the algorithm might look like this...
1. Find common prefix for first two strings
2. Check if the third string shares the common prefix
3. If no,
4. Find the common prefix for the first and third string
5. Repeat 2-4 for the remaining strings
It looks pretty okay, except that programming is often a stubborn process and trivial things doesn't seem to happen naturally in computers. So, to simplify it for programming, we can first assume that the common prefix is the first string. Then, we find the common prefix for the assumed common prefix and the other strings, and we update the assumed common prefix as we go. So in the end, we will have the assumed common prefix as the correct common prefix, since we have chopped it over and over again as we check through all the strings, making sure that it is the common prefix we are looking for.
So, the algorithm can look like this in human language...
1. Assume that the first string is the common prefix
2. Check if the assumed common prefix and the second string shares a common prefix
3. If no,
4. Update the assumed common prefix with the common prefix for the assumed common prefix and the second string.
5. Repeat 2-4 for the remaining strings
6. Return the assumed common prefix as the result
There, it looks more like a program now. With a line saying what we need to return too. However, it is still going to be troublesome to program, because we have to make checking and updating to be separate steps, and we don't like writing much code, especially unnecessary code... how about we just update the assumed common prefix without checking anyway? Since if we update a correct value with another correct value, it'll still be correct. Besides that, checking the common prefix and updating the assumed common prefix pretty much share the same steps, so let's just simplify it more...
1. Assume that the first string is the common prefix
2. Update the assumed common prefix with the common prefix for the assumed common prefix and the second string
3. Repeat 2 for the remaining strings
4. Return the assumed common prefix as the result
Looks pretty good, let's implement it into a program then.
I use the C# language, and in this program, res is my result, which is also known as the "assumed common prefix" from the algorithms above. To update the assumed common prefix, I use a loop to go through each character in the strings from their start, and if the characters from the two strings match, they are added to the new assumed common prefix, and if they don't match, that means we are done finding the prefix, and should break away from the loop and continue with the next string.
I also added two cases where the program can immediately return the answer without computing - if the array of strings is empty, then the program can just return a null (meaning "pointing to nothing" in computers), since there can't be a common prefix if there are no strings; and if there is only one string in the array, then the program will just return the string as the answer, as the string itself must be the longest prefix available, since no other strings could affect it!
public class Solution {
public string LongestCommonPrefix(string[] strs) {
if (strs.Length == 0) return null;
if (strs.Length == 1) return strs[0];
string res = strs[0];
for (int j = 1; j < strs.Length; j++) {
StringBuilder newres = new StringBuilder();
for (int k = 0; k < Math.Min(res.Length, strs[j].Length); k++) {
if (res[k] == strs[j][k]) newres.Append(res[k]);
else break;
}
res = newres.ToString();
}
return res;
}
}
I call this approach "the naïve approach", as really, there's nothing fancy about it - it's just about going through all and every string, updating the common prefix as we go, and finally getting the correct answer. Complexity wise, it isn't bad, with the worst case being O(S) where S is the total number of characters in the string array. In fact, looking at the solutions available online, it might be one of the faster ones available to solve the problem, although to be frank I'm not very sure if there are significantly slower algorithms available for this problem. Unless we stick with the first idea of checking and then updating, then... maybe.
After having the program, it's time to test - but how? It's hard to test against all possible cases with all the edges covered, but there is a simple way... you see, obviously, this question is on Leetcode. I don't really like Leetcode (I don't know why), but having the problem there makes testing easier, because we just need to paste the thing in and it'll do the rest.
So pasting it in... and it got accepted, great!
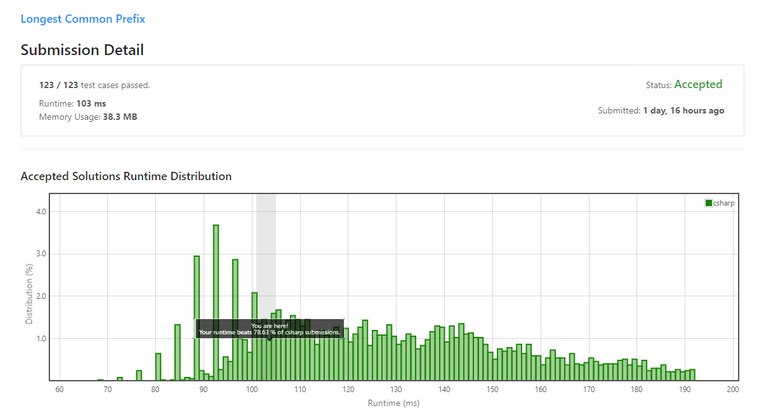
Well, as you can see, it isn't terrible. Speed wise and memory consumption wise it's above average, and in terms of theoretical complexity (which is O(S) as mentioned above), it's also pretty good. So we're done, right?
I thought so... but I personally don't really like this approach. It works, but with nested for loops and you have to go through all the strings. Plus, it's really naïve, which makes it not that satisfying to implement. There should be some other way which I can do this more cleanly, right? Other than the other few really good approaches we can see in Leetcode's solution page?
Turns out that, there seems to be really something else that I can do...

If you ever tried sorting files by their names on your computer, you might have noticed this: File names are typically sorted in a pattern like, "aa, ab, ba, bb, cdz, ce, ...". That is quite how strings are sorted - if ascendingly, they go alphabetically, and the size of the "differences" goes down the further behind the characters in the string that are different.
Another way to look at it is by treating strings as floating numbers. For example, to sort "ab", "aaaa" and "abcd", we can treat them as floating numbers like 0.12 for "ab", 0.1111 for "aaaa", and 0.1234 for "abcd". When you sort them ascendingly, you'll get 0.1111, 0.12, 0.1234, and hence the result is "aaaa", "ab", "abcd". Of course, you can't extend this directly to support all 26 different alphabets (and we aren't even looking at the ASCII or even Unicode tables yet), but the idea is there.
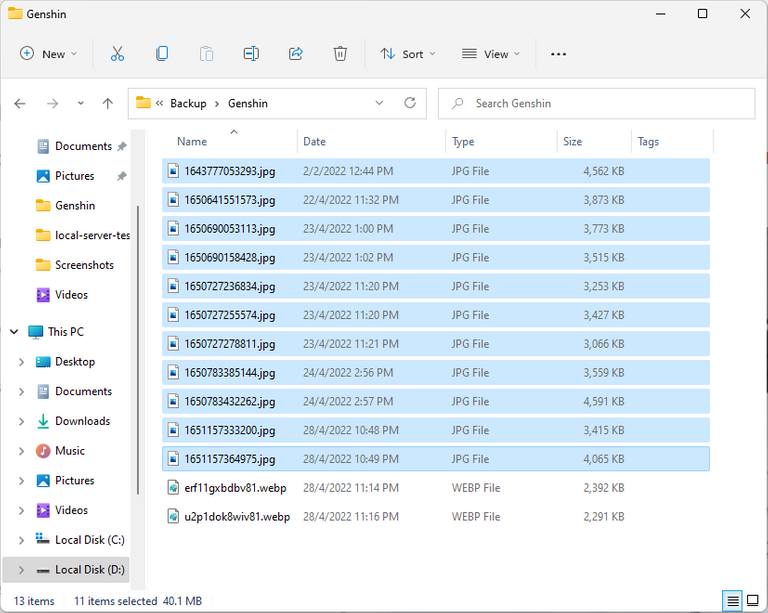
So... how do we abuse this? If you notice in the picture above (the highlighted files), after sorting, the first string in the array will have the largest difference with the last string. If they have a common prefix, then the rest of the strings in the array must also share the common prefix - since they are all sorted and will not have larger differences than those two strings! Hence, to find the common prefix from an array of strings, it is possible to just sort those strings, and find the common prefix for the first and the last string.
And the good news is, on almost all modern programming languages, sorting is a built-in function. In C#, to sort an array of strings, all we need do is just do Array.Sort(strs);, where strs is the array of strings. That'll take care of it, no need for dealing with recursion or googling about the quicksort algorithm, and you can't accidentally implement bubble sort either.
Hence, the code...
public class Solution {
public string LongestCommonPrefix(string[] strs) {
Array.Sort(strs);
StringBuilder prefixBuilder = new StringBuilder();
for (int i = 0, j = strs.Length - 1, k = Math.Min(strs[0].Length, strs[j].Length); i < k; i++) {
if (strs[0][i] == strs[j][i]) prefixBuilder.Append(strs[0][i]);
else break;
}
return prefixBuilder.ToString();
}
}
And Leetcode accepts it :)
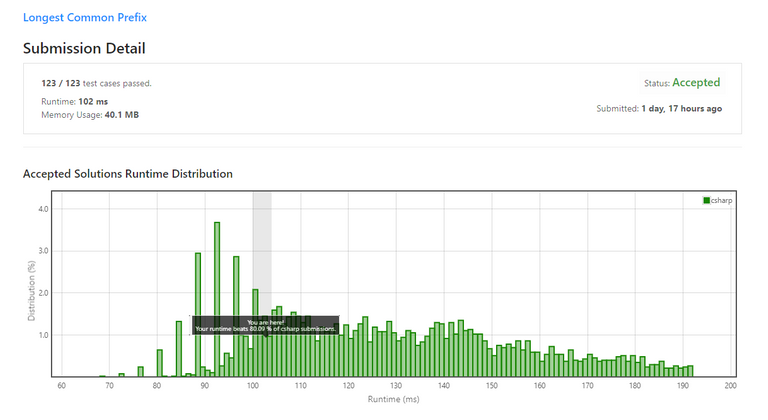
It looks not bad. Memory usage is not that impressive, probably because C# uses an insertion sort algorithm for sorting small arrays with Array.Sort(), and this algorithm uses additional memory to work. Looking at the runtime, it is somewhat similar to the first approach I tried. Interesting, since theoretically, it should have been worse.
Why worse? Because apparently, the operation of sorting the strings should have a complexity of about O(S*n log n), which I learned from this CS StackExchange thread. The operation of building the prefix is not significant enough to affect the overall complexity, but it should be easily tellable that O(S*n log n) is worse than O(S). But why the performance looks similar? Personally I guess it's because that Leetcode's test input sets are not large enough to make the sorting be slow, so it didn't made a visible difference. It's pretty horrible when we do the maths, but on the graphs, it looks okay-ish.
I ended up submitting this approach involving sorting, but well, I will have to explain that it actually is a bad idea in practice if I got asked about it. I should also go back to the solution page on Leetcode to study some of the other approaches listed there, some of them are pretty interesting as well. Like the one that uses binary searching, I think I should learn how that actually works. Might be useful someday.
That's all for now? See you next time.
:)