How to calculate the relative extrema of a cubic function by applying the criterion of the first derivative?

Hello friends and followers of STEM content, this time I want to share with you how we can calculate the relative extrema (maximum point and minimum point) of a cubic function by applying the criterion of the first derivative.

To do this the proposal is to find the maximum and minimum point of the following cubic function:

Why is it necessary to use the criterion of the first derivative to know the maximum and minimum points of the cubic function?

The cubic function will have a behavior where it grows and reaches the highest point and then decreases and reaches the lowest point and then grows indefinitely to infinity. Logically we find the images of the function, i.e. we give arbitrary values to the variable x to know its image f(x).

However with these values of the images we can be left inconclusive the cuts with the coordinate axes X and Y, and also we are left inconclusive the coordinates of the maximum and minimum points of the cubic function.

If we use a software that allows us to introduce the equation of the cubic function we will be able to know the cuts with the coordinate axes and the coordinates of the maximum and minimum points, we will also be able to deduce its behavior. For this case I have used the software geogebra in its last version, when we open the application we see something like this:

Then we enter the equation of the cubic function using the digital keyboard tools displayed by the program:

The graph is then displayed on the right side, as shown below:

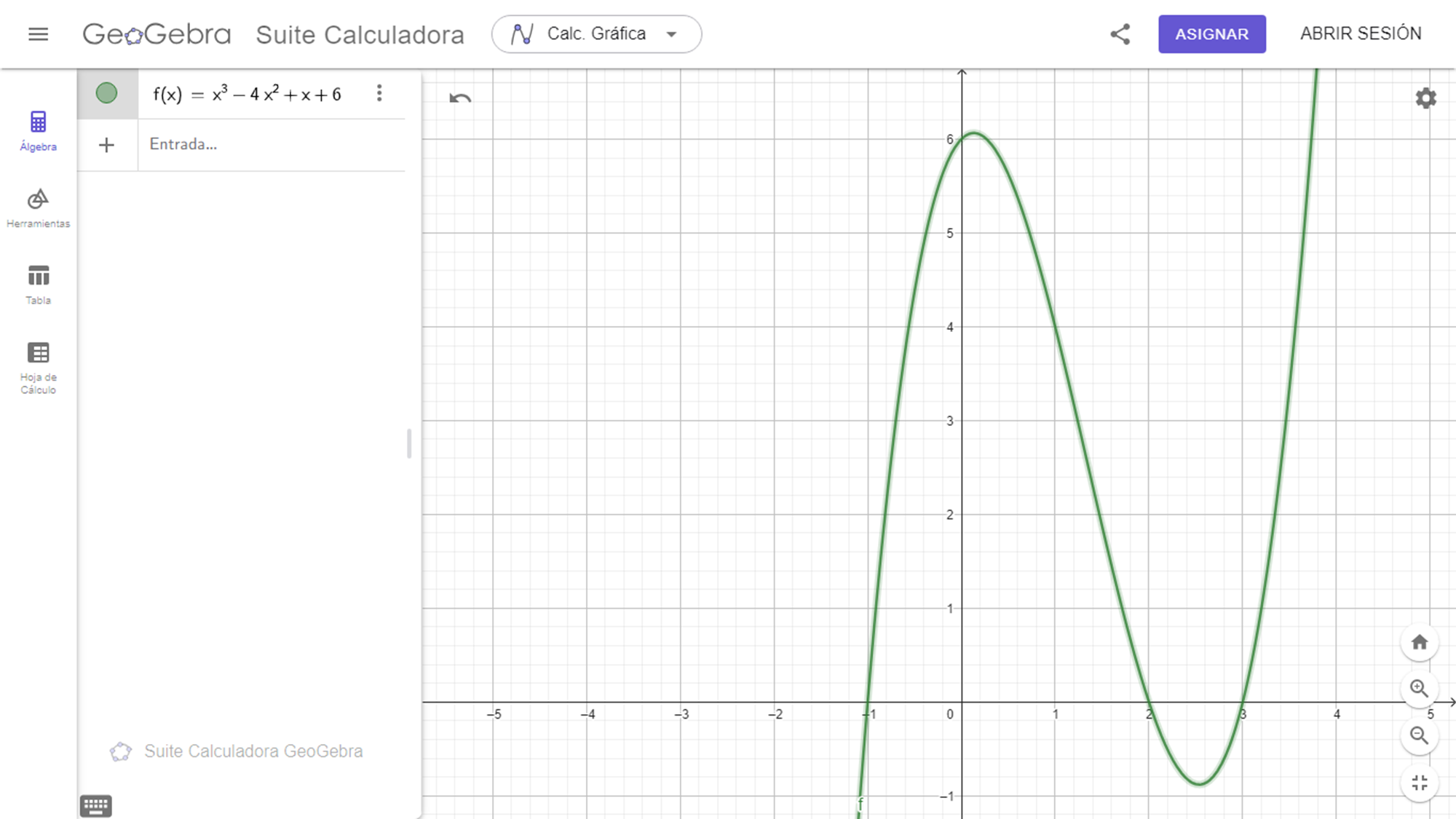
Already with the graph produced by the geogebra program we can see that the cubic function cuts the x-axis at:

X= -1
X=2
X=3

We can also see that the cubic function cuts the y-axis at:

Y= 6.

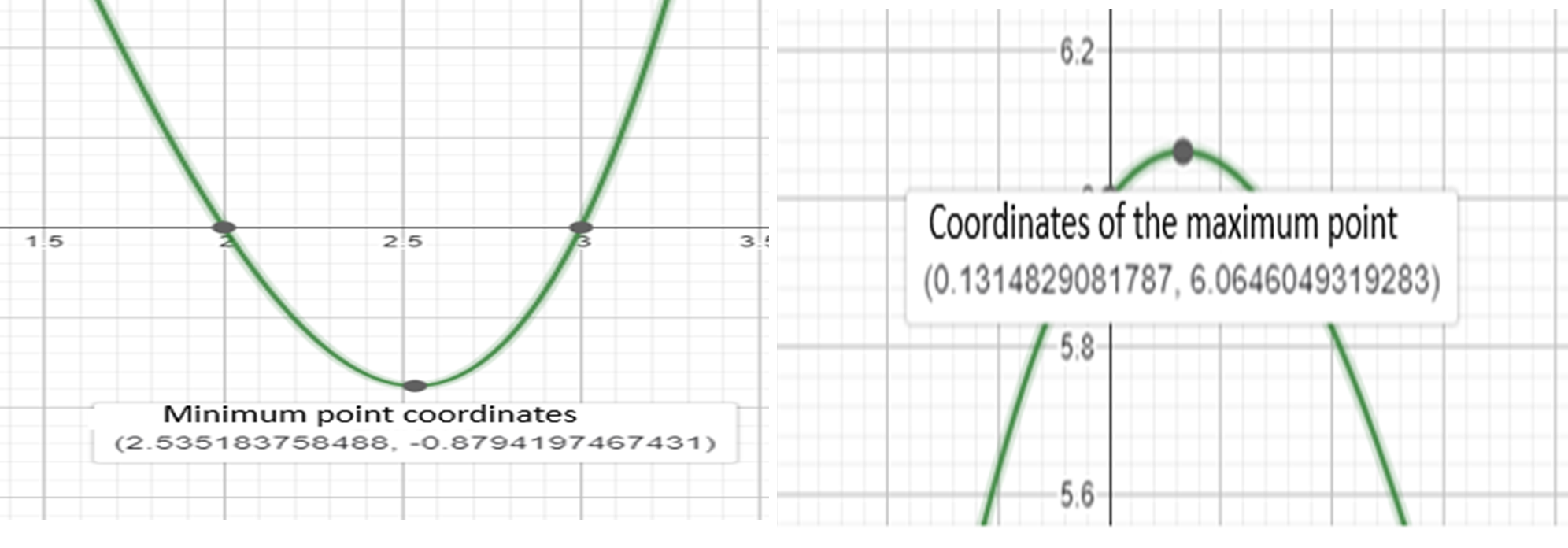
The coordinates of the maximum point are:

[0.131 ; 6.06]

The coordinates of the minimum point are:

[2.53 ; -0.879]

Is it possible to know the coordinates of the relative extrema of this cubic function by means of another tool?

Of course, which is the purpose of this post, assuming that we do not have at the moment some mathematical software, we can calculate the relative extrema of a cubic function with the criterion of the first derivative.

The criterion of the first derivative what it states is that when we equal the first derivative to zero and we solve the factorization of the polynomial that we have left, the values found are going to be the coordinates in X of the maximum point and the minimum point, therefore we proceed as follows:

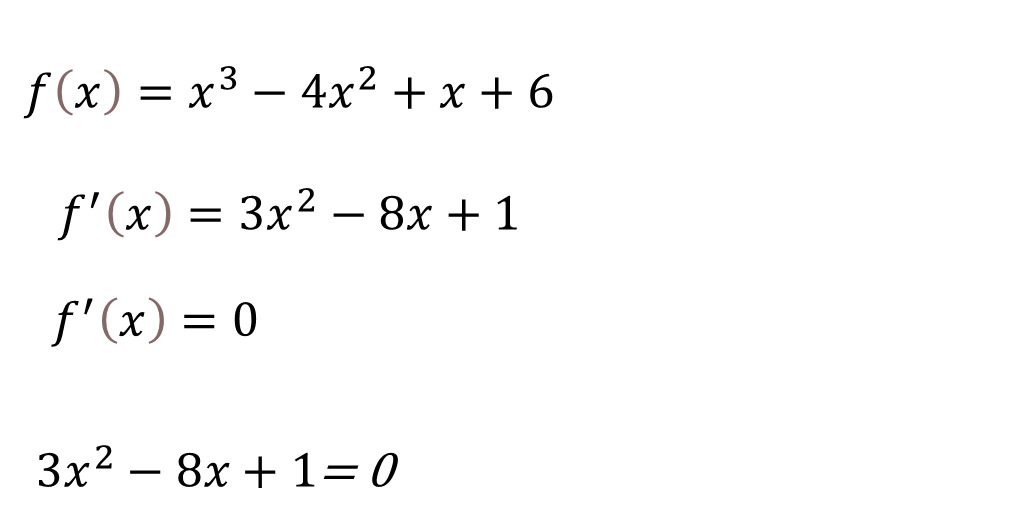
If we find the solution of the second degree equation, we can use the resolvent formula:

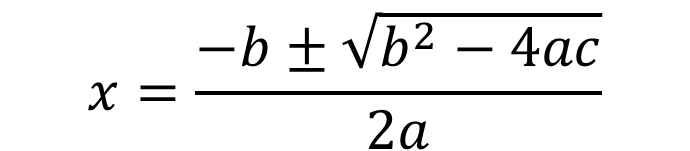
To this end:

a= 3
b= -8
c= 1

Therefore:

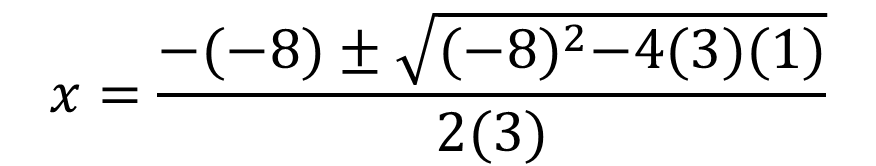
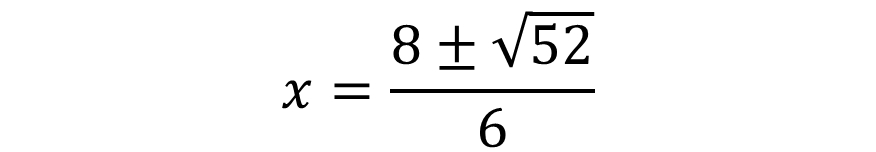
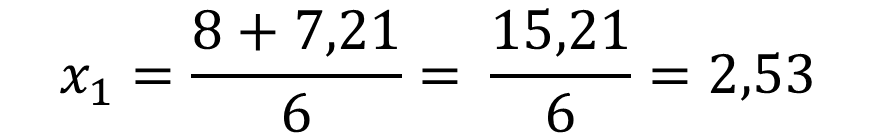
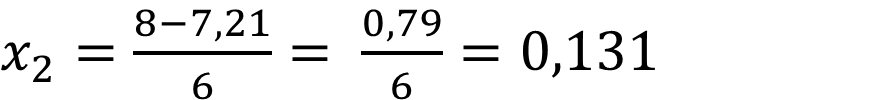
To find the Y-coordinate of the maximum and minimum points, we substitute in the cubic function the value of the X-coordinates of X1= 2.53 and X2= 0.131.

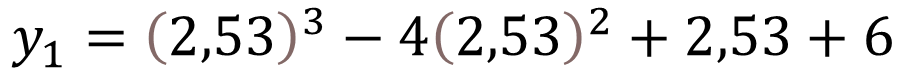
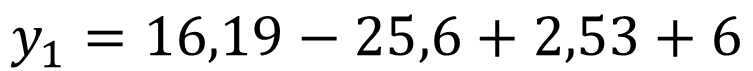
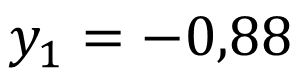
Therefore the coordinates of the minimum point is:

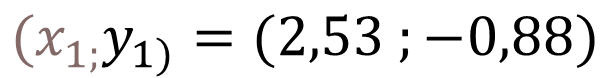
For the maximum point we substitute X= 0.131 in the cubic function:

Therefore the coordinates of the maximum point are:

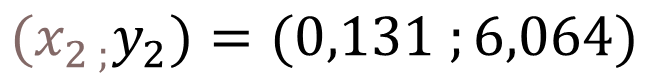
The conclusion to find the relative maxima of a cubic function is that if we do not have a mathematical program or software at hand, we must know that we have the criterion of the first derivative to get the coordinates of the maximum and minimum points of the function.

Recommended bibliographic references

Book of calculus with analytic geometry volume I. Author: Larson and Hostetler. 7th edition. Year 2007.

Note: The images of the cubic function graphs were generated with geogebra software and edited with Microsoft PowerPoint. The equations were elaborated using the equation insertion tool of Microsoft PowerPoint.