| Español | English |
Enunciado
Solución
x + 1/x = √ 2 , |
|---|
Este problema se puede resolver empleando las propiedades de las funciones simétricas.
Una función es simétrica, si intercambiando cualesquiera de sus variables el valor de la función no varía |
x = α , 1/x = β
α + β = √ 2
α ∙ β = 1
Como es bien conocido, relaciones de Cardano-Vieta , α y
β son raíces de la ecuación,
ξ 2 − √ 2 ∙ ξ + 1 = 0
α = √ 2 /2 ∙ ( 1 + i ) = е i ∙ π/4
β = √ 2 /2 ∙ ( 1 − i ) = е − i ∙ π/4
Sólo resta evaluar α y β elevadas a la 777 potencia,
777 = 4 ∙ 194 + 1
е π ∙ 777/4 = е π ∙ 194 ∙ е π/4 = е π ∙ 2 ∙ е π/4 = е π/4
∴ x 777 = x
De dónde,
1 |
|---|
∎
| English | Español |
Statement
Answer
x + 1/x = √ 2 , |
|---|
This is a problem on symmetric functions.
A function is symmetric if the exchange of its variables does not alters its value |
x = α , 1/x = β
α + β = √ 2
α ∙ β = 1
As it is well known, Vieta's formula , α and
β are roots of the equation,
ξ 2 − √ 2 ∙ ξ + 1 = 0
α = √ 2 /2 ∙ ( 1 + i ) = е i ∙ π/4
β = √ 2 /2 ∙ ( 1 − i ) = е − i ∙ π/4
Evaluating α and β to the 777 power,
777 = 4 ∙ 194 + 1
е π ∙ 777/4 = е π ∙ 194 ∙ е π/4 = е π ∙ 2 ∙ е π/4 = е π/4
∴ x 777 = x
Whence,
1 |
|---|
∎
Media
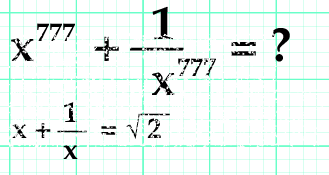
Congratulations @j2e2xae! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 900 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOP