Hello math bugs(🐞) and hivers(🐝)
Well come to another interesting proof of geometric formula, volume of a cone [1/3 πr²h]!
We all get to know about volume of a cone in school but we just crammed the formula without knowing where from it comes. Many times it came to my mind but I didn't have the answer then. Later asvstudy progress, we come to know the actual reason how or why it is 1/3 of volume of right circular cylinder of the same radius of circular base.
We may vidualise it with 3D photos or we may find the formula of the volume of a cone by temparing its shape but Today I won't do that. I am going to proof it using calculas(integration) only. 😀 Let's begin
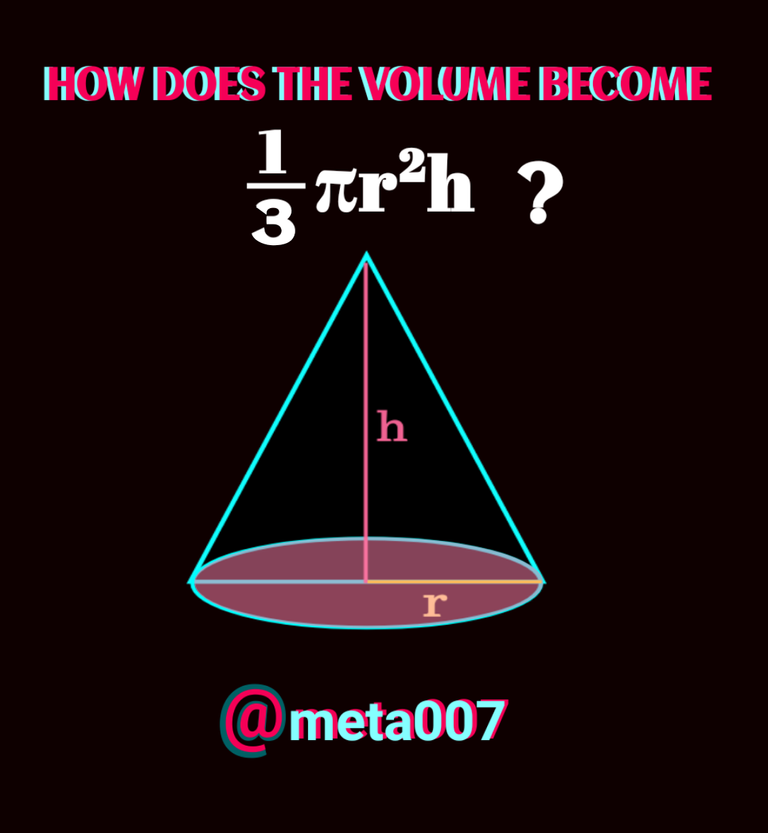
Let's put it on x and y plain:
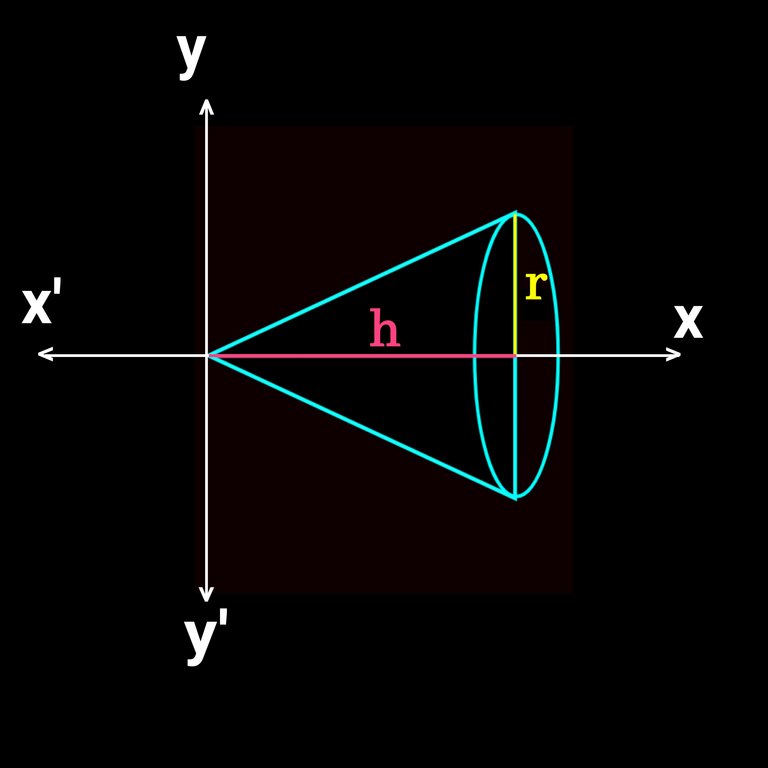
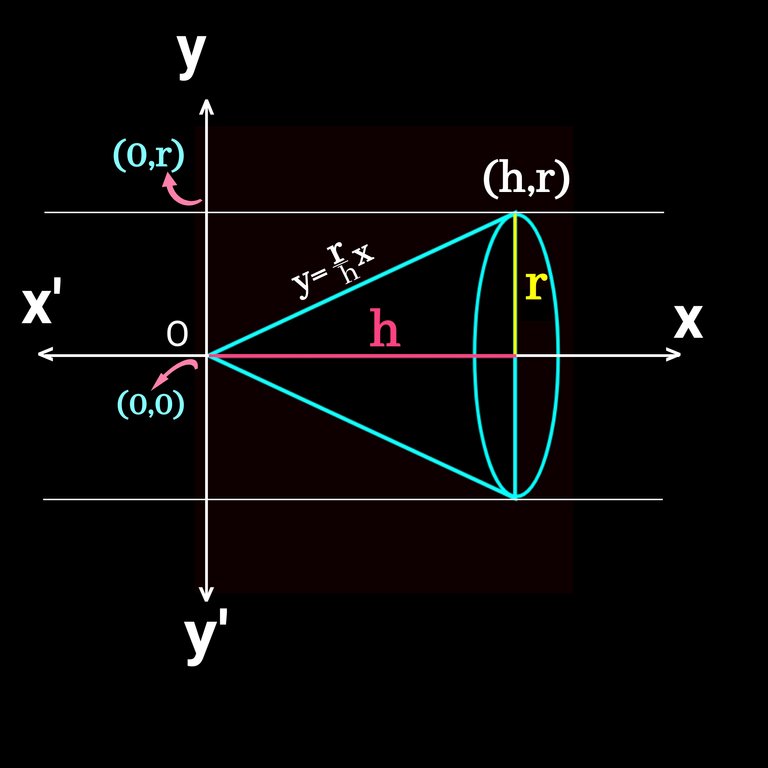
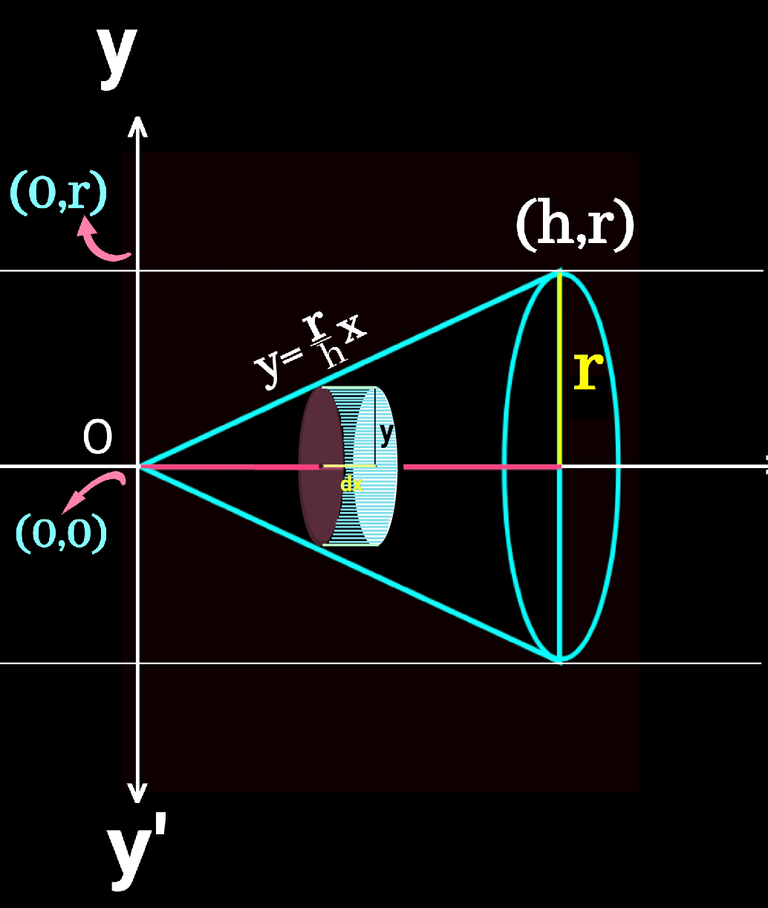
I like to put the vertex of the cone at origin (0,0) for easier calculation. If we take radius of base r units and the height h unit, after putting in the plain we get the following figure.👇Here we take height on the X axis and radius on the Y axix.
Now look at the green part in the following figure. It's base is a very negligible distnace on the X axis denotaed by dx and the height given by y.
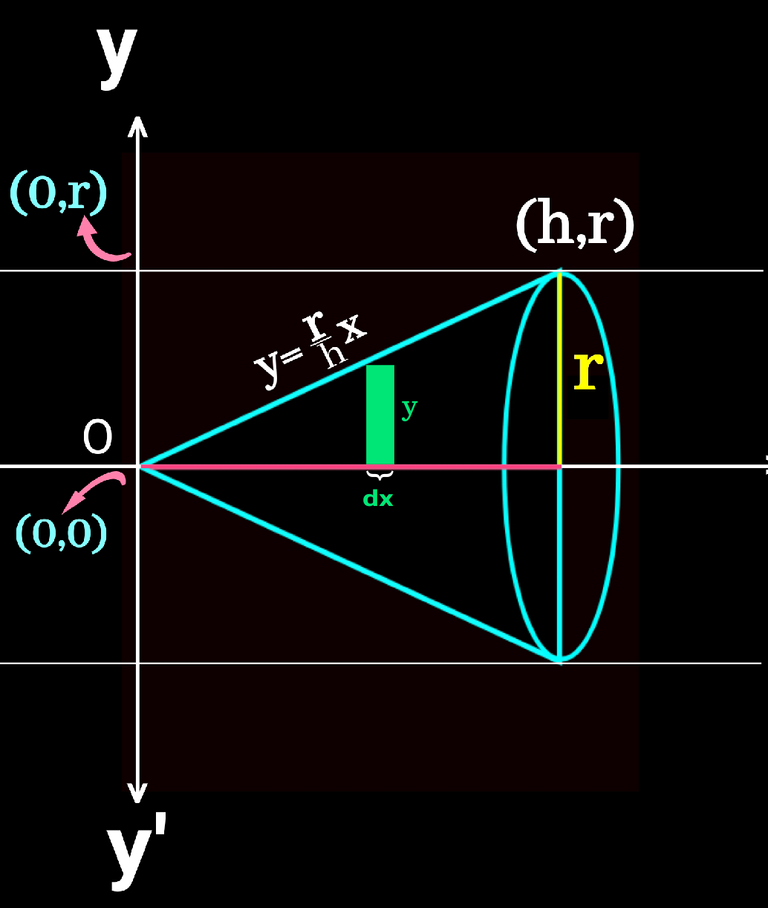
Let try to understand the green portion in 3d view on both side of x axis and thus we get a very little cylindrical shape with radius of its base y and height again the smallest distance called dx on x-axis. Check it below👇
Not vivid! Let's zoom it

Area of the cylindrical shape will be actually dv means volume of very small part the original cone. If we integrate dv, we get volume of the cone. Let's do it.

Here y= rx/h is the equation in slope form of the slaint height of the cone on the first quadrant of the cartatian plain. As our integration is in x world , here, we have to convert y into x with π, the constant are r and h. So we take them out of intregration part. Finally we intregate x² and when we intregate it, we get another constant 1/3. This what I wanted to show you. How that 1/3 comes in the volume of a cone.
For any querry, you can hit a comment right below.
🎤🎤 All the figures used here are made by me. There may be some silly mistakes; please try ignoring them. The drawing may not be accurate, I am sorry for that.
I hope liked it
Thanks for stopping by
Have a nice day
All is well
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.