7-4 초보자를 위한 Anaconda3 선형회귀문제 단순 파이선 코딩 연습문제

이 연습 문제는 PyTorch 머신 러닝을 익히기 전에 해보는 단순한 파이선 코딩에 의한 선형회귀 문제의 계산 및 그래픽 처리 과정이다. PyTorch 라이브러리 설치 이전에 Anaconda TensorFlow 설치 과정에서 종속적인 라이브러리 모듈로서 numpy 와 matolotlib 가 이미 설치되어 있음을 상기하자. 물론 윈도우즈 7 버전에서는 Python 3.6 버전을 3.5 버전으로 대체하는데 실패하여 아나콘다에서 TensorFlow를 사용할 수는 없지만 PyTorch 와 numpy, matplotlib 모듈을 사용함에는 아무런 문제가 없다.

import numpy as np
import matplotlib.pyplot as plt

Linear regression 유형의 머신 러닝 코드를 다루기 위한 전초 작업으로서 Linear regression에서 다루게 될 리스트 데이터를 설정해서 워밍업을 해보자.

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

두개의 함수를 설정해 보자.
다음의 forward(x) 함수에서 x 값이 주어지면 웨이트 w 는 따로 그 값이 주어져야 계산 결과를 되돌려 줄 수 있다. 뒤따르는 코딩에서 w를 어떻게 처리 하는지 유심히 살펴보자.

def forward(x):
return x * w

다음의 함수 loss( x, y)는 TensorFlow에서 최소제곱법 계산 루틴과 유사하다. x 값이 주어지면 웨이트 w 는 어디선가 주어질 것으로 본다. y_pred 계산이 가능하며 아울러 학습 값 y 가 함께 주어지면 y-pred 와 y 와의 차이 값의 제곱을 계산하여 되돌려 줄 수 있다.

def loss( x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred – y)

두 개의 리스트형 데이터 변수를 설정해 두자. numpy 든 matplotlib 든 항상 리스트형 데이터를 즐겨 사용함에 유의하자.

w_list = []
mse_list = []

자 드디어 웨이트 w 가 for arange 형태로 나타난다. 그 범위를 0.0에서 4.0까지로 두고 0.1 만큼 씩 증가시켜 보자. 일단 웨이트 w를 출력 후 l_sum 값을 0.0 으로 세팅 한다.

for w in np.arange(0.0, 4.1, 0.1):
print("w=", w)
l_sum = 0

이 상태에서 다음과같이 for zip 명령을 사용하여 준비했던 데이터 수만큼 loop를
실행시키자. zip(x_data, y_data)은 각각의 리스트 데이터 순번대로 하나씩 뽑아 x_val, y_val에 값을 부여한다.

for x_val, y_val in zip(x_data, y_data):

x_val값을 입력으로 하여 함수 forward를 불러 계산한 값을 y_pred 로 둔다.
이때에 forward를 부르면 w 값은 이미 저 위의 선행하는 for loop에서 이미 값이 주어진 상태이므로 함수 forward에서는 상수처럼 여겨진다. forward(x_val) 값을 계산하여 y_pred_val로 두는 까닭은 loss 함수를 호출하면 그 속에서도 계산하지만 아마도 별도로 출력해보기 위해서 계산하는 것이다. loop를 돌면서 계속 loss를 계산하여 합해둔다.
y_pred_val = forward(x_val)
l = loss(x_val, y_val)
l_sum += l
print("\t", x_val, y_val, y_pred_val, l)

for loop에서 한번에 0.1 만큼 증분하면서 주어지는 w 값에 대해서 계산된 l_sum 값을 데이터 수인 3으로 나누어 평균값을 출력해 본다. 각각의 웨이트값 w와 loss 의 평균값을 미리 설정해두었던 두 개의 리스트에 담아 둔다.
print("MSE=", l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)

준비된 리스트 데이터를 사용하여 matplotlib 모듈을 사용하여 플롯해보자.
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

셸(Shell) 계산 값 출력 결과 -----------------------------------
w= 0.0
1.0 2.0 0.0 4.0
2.0 4.0 0.0 16.0
3.0 6.0 0.0 36.0
MSE= 18.666666666666668
w= 0.1
1.0 2.0 0.1 3.61
2.0 4.0 0.2 14.44
3.0 6.0 0.30000000000000004 32.49
MSE= 16.846666666666668
∙∙∙
w= 4.0
1.0 2.0 4.0 4.0
2.0 4.0 8.0 16.0
3.0 6.0 12.0 36.0
MSE= 18.666666666666668
셸(Shell) 그래픽 처리 출력 결과__________________________

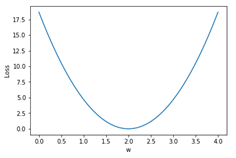
계산 결과를 보니 웨이트 값 w = 2.0 일 때에 최소값을 가짐을 알 수 있다. 이런 방식의 계산은 텐서플로우나 파이토치 라이브러리 지원 없이도 단순 파이선 코딩으로 가능하다. 다음 단계에서는 선형 회귀법 형태로 파이선 코딩을 해보기로 한다.

#Just _python_code
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

def forward(x):
return x * w

def loss( x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)

w_list = []
mse_list = []

for w in np.arange(0.0, 4.1, 0.1):
print("w=", w)
l_sum = 0

for x_val, y_val in zip(x_data, y_data):
    y_pred_val = forward(x_val)
    l = loss(x_val, y_val)
    l_sum += l
    print("\t", x_val, y_val, y_pred_val, l)
    
print("MSE=", l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)