Elements of Set Theory: Equivalence Relations

Consider a set A given by a figure in (a), say we want to partition it into six boxes as in (b).

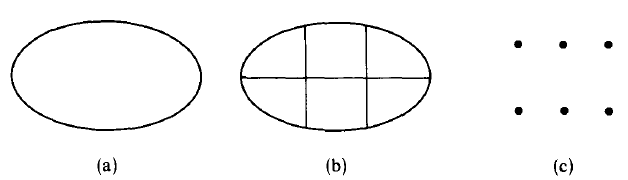
For example, take, we can partition into six parts:

By partition we mean, dividing the box into a similar box such that each is a nonempty subset of A. Now let's inject some kind of mental agility into this simple mental exercise, instead of thinking of the partition as a plurality of objects think of each box as a single object - (we've been doing this in the previous sections we've covered by thinking of a set as a single object) - each box is now, in our mind, a single point as in figure (c).

We call this set of points as set B while the original set as A. It is easy to see that while the former set B is finite, consisting only of six members the original set is infinite.

This process of transforming a situation like in A into a set B is common in abstract algebra and elsewhere in mathematics. And the future chapters (5), the process will be applied several times in the construction of the real numbers.

Now consider a binary relation on A as follows,

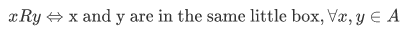
We can say that R has the following properties:

R is reflexive on A, by which we mean that 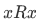for all .
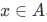R is symmetric, by which we mean that whenever 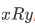, then also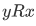
R is transitive, by which we mean that whenever 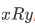and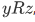, then also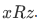

With these properties we can now define equivalence relation.

Definition R is an equivalence relation on A iff R is a binary relation on A that is reflexive on A, symmetric, and transitive.

Theorem 3M If R is a symmetric and transitive relation, then R is an equivalence relation on fld A.

Note that: fld A = .

Proof:

any relation R is a binary relation on its field, since

our goal is to show that R is reflexive on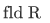

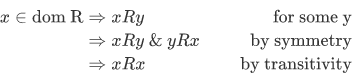
and similar calculation work for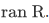

A precautionary note:

If R is symmetric and transitive relation on A, it does not follow that R is an equivalence relation on A. R is reflexive on fld R, but fld R may be a small subset of A.

Definition The set 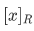is defined by

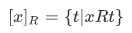
If R is an equivalence relation and 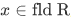, then 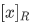is called the equivalence class of x (modulo R). [refer to (properties of relations) of giam]. A fixed relation R is written just .

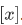Lemma 3N Assume that R is an equivalence relation on A and that x and y belong to A. Then

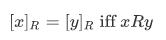
Definition A partition of a set A is a set of nonempty subsets of A that is disjoint and exhaustive, i.e.,

a) no two different sets in 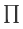have any common elements, and

b) each element of A is in some set in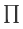

Theorem 3P Assume that R is an equivalence relation on A. Then the set of all equivalence classes is a partition of A.

If R is an equivalence relation on A, then we can define the quotient set

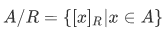
whose members are the equivalence classes. We also have the natural map (or canonical map: 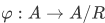) defined by

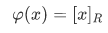
Theorem 3Q Assume that R is an equivalence relation on A and that 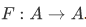. If F is compatible with R, then there exists a unique 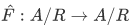such that

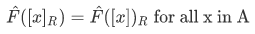
We say that F is compatible with R iff for all x and y in A,

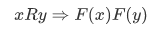
^{Disclaimer: this is a summary of section 3.6 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora}

Elements of Set Theory by Herbert B. Enderton

Thank you for reading ...