
Regularność od zawsze sprawia na nas duże wrażenie. Regularność, którą możemy odnaleźć w geometrii płatka śniegu, architekturze, równaniach, czy w sztuce. Symetria w jakiś tajemniczy sposób wpływa na przyjemność naszych doznań wzrokowych. Nie zastanawiajmy się jednak dlaczego tak się dzieje. Zastanówmy się nad tym czym jest symetria. Zadajmy sobie zatem pytanie:
Pytanie to brzmi trywialnie i rzeczywiście takie jest. Intuicyjnie możemy wnioskować który stół wykazuje większą symetrię. Myślę, że Twoja odpowiedź brzmiałaby: okrągły stół. Moja odpowiedź byłaby identyczna. Problem pojawia się jednak, gdy spytamy dlaczego. Pozwól, że spróbuję to Tobie wyjaśnić.
Skoncentrujmy się na kwadratowym stole.
Wyobraź sobie, że jesteśmy w pokoju, a przed nami stoi kwadratowy stoliczek. Wychodzisz z pokoju, lecz doskonale pamiętasz jakie było jego pierwotne ustawienie. Po chwili wracasz do pokoju. Ja natomiast w międzyczasie zmieniłem ustawienie stolika obracając go. Możliwe są dwa scenariusze. Jeżeli obrócę stolik o powiedzmy 45 stopni, zauważysz, że zmieniło się jego ustawienie. Wierzchołki stolika będą w innych miejscach niż pierwotnie. Mogę też obrócić stolik o powiedzmy 90 stopni, a wtedy nie zauważysz różnicy między aktualnym, a pierwotnym ustawieniem. Wierzchołki zamienią się miejscami, lecz stolik będzie stał identycznie jak przed Twoim wyjściem. Zapamiętaj ten przykład. Przechodzimy teraz do matematyki.
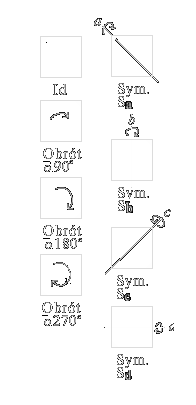
Istnieje prężnie rozwijająca się dziedzina matematyki, która bada własności struktur algebraicznych zwanych grupami. Jej zastosowanie jest nadzwyczaj szerokie w wielu dziedzinach nauki i nie tylko. Nosi ona nazwę teorii grup. Żeby nie atakować Ciebie czystą matematyką, rozpatrzymy pewien przykład, który powinien wystarczająco jasno przedstawić o co chodzi. Weźmy kwadrat. Każdy wie czym charakteryzuje się kwadrat. Możemy wykonywać na nim różne działania. Mogę dla przykładu obrócić go o 180 stopni względem środka, lub odbić symetrycznie względem osi poziomej. Te działania nazywają się przekształceniami. Obrazek obok przedstawia przekształcenia kwadratu. Badając je możemy zauważyć kilka ciekawych własności.

I. Jak wyżej możemy obrócić kwadrat o 90 stopni, 180 stopni, czy 270 stopni. Wierzchołki kwadratu będą wtedy zamieniać się miejscami. Jeżeli natomiast obrócimy kwadrat o 360 stopni to nic się nie zmieni. Wierzchołki pozostają na swoim miejscu. Obrót ten jest równoważny obrotowi o 0 stopni, to znaczy braku przekształcenia (w matematyce nawet brak działania jest działaniem). Przekształcenie, które nie zmienia ustawienia badanej figury nazywa się przekształceniem identycznościowym (Id)

II. Możemy też składać przekształcenia. Najpierw obrócić kwadrat o 90 stopni, po czym obrócić o 180 stopni. Złożenie to jest równoważne obrotowi o 270 stopni. Możemy też obrócić kwadrat o 180 stopni, a następnie odbić względem osi pionowej. Złożenie to jest równoważne odbiciu względem osi poziomej. Tabela obok przedstawia wszystkie złożenia przekształceń, które ukazane zostały powyżej. Zauważmy, że dowolne złożenie jest równoważne z którymś z 8 wymienionych przekształceń. Nigdy nie dostaniemy przekształcenia, które nie należy do zbioru wybranych przez nas przekształceń. Własność ta jest nazywana zamkniętość lub wewnętrzność.
III. Zauważmy, że jeżeli obrócimy kwadrat o 90 stopni a następnie o 270 stopni, to złożenie to równoważne jest przekształceniu identycznościowemu (Id). W tym przypadku obrót o 270 stopni jest przekształceniem odwrotnym do obrotu o 90 stopni. Okazuje się, że każde wymienione wyżej przekształcenie posiada przekształcenie odwrotne (sprawdź tabelkę). Własność ta to odwracalność.
IV. Weźmy trzy dowolne przekształcenia w określonej kolejności. Niech będzie to: obrót o 90 stopni - odbicie względem osi pionowej- obrót o 180 stopni. Równoważne jest to odbiciu względem przekątnej. Jeżeli teraz weźmiemy te same przekształcenia, lecz w innej kolejności: odbicie względem osi pionowej - obrót o 180 stopni - obrót o 90 stopni, również jest to równoważne odbiciu względem przekątnej. Jest to spełnione dla dowolnych przekształceń. Kolejność wykonywanych przekształceń nie ma znaczenia. Własność ta nosi nazwę łączności.
W teorii grup, zbiór (u nas zbiór przekształceń) wyposażony w działanie (u nas działanie złożenia przekształceń) spełniający cztery powyższe własności nazywamy grupą. No dobrze, lecz poczekajmy na chwilę. Czemu nie uwzględniłem takich przekształceń jak obrót o 45 stopni, czy odbicie względem dowolnej osi? Gdyby należały one do naszego zbioru przekształceń również mielibyśmy do czynienia z grupą. Przypomnij sobie teraz kwadratowy stoliczek w pokoju. Wybrałem tylko takie przekształcenia, które nie zmieniają ustawienia stolika! To bardzo ważne. Tak zdefiniowana grupa, która składa się tylko z izometrii przekształcających figurę w siebie nazywamy grupą symetrii. To jest klucz do zrozumienia symetrii.
Grupa symetrii kwadratu składa się z ośmiu przekształceń. Ilość elementów (przekształceń) grupy nazywamy rzędem grupy. Analogicznie w teorii mnogości definiujemy moc zbioru, czyli ilość elementów należących do zbioru.
Wróćmy zatem do naszego pytania z początku artykułu. Stół kwadratowy mamy już za sobą. Ze stołem okrągłym uporamy się natychmiastowo. Ile istnieje przekształceń okrągłego stołu, które nie zmieniają jego położenia? Nieskończenie wiele! Możemy dokonać obrotu o dowolny kąt, a także dokonać odbicia względem dowolnej osi. Rząd grupy symetrii okręgu jest zatem nieskończony. Dlatego właśnie stół okrągły jest bardziej symetryczny niż kwadratowy. Co więcej bardziej symetryczny niż dowolny wielokąt foremny.
Dziękuję za poświęcenie uwagi i zapraszam do innych artykułów.
troche to skomplikowane ale interesujące :D
Regularnie to ja zamierzam czytać Twoje posty. Najlepiej z rana, na 'przebudzenie' i odrobinę zachwytu nad estetyką nauk ścisłych.
Oo dziękuje. Bardzo mi miło :D Zazwyczaj pisze po nocach. Syn w ciągu dnia daje popalić.
Świetnie wytłumaczone!
Co za genialny post
The Vote For Your Awesome Post Has Just Arrived!
NOVOTES.SteemiTag is an innovative program that helps users increase their gains in the curation rewards by voting on posts that are likely to get high payouts. It maximizes the chance of a user to be rewarded through an accurate selection algorithm that works 24/7 and eliminates "no rewards" problem for users with low Steem Power. You can participate in our program by clicking on this link and confirming your delegation. Your rewards will be sent to you in the form of weekly dividends. Thank you and keep up with your great work!
Ten skarb został odkryty dzięki OCD Team! Odpisz na ten komentarz jeśli zezwalasz na podzielenie się nim z innymi! Akceptując to masz szanse na otrzymanie dodatkowej nagrody i jedno z twoich zdjęć z artykułu może zostać wykorzystane w naszej kompilacji postów! Możesz śledzić @ocd - i dowiedzieć się więcej na temat projektu i zobaczyć inne skarby! Dążymy do przejrzystości.
Zezwalam.