Introducción
Hola amigos, en esta oportunidad quiero compartirles un pequeño experimento que realicé para comprobar un teorema matemático bastante conocido por quienes están familiarizados con la geometría:
La suma de los ángulos interiores de un triangulo suman 180°
Si bien es cierto que es un teorema matemático que cuenta con demostración, me llamó la atención el hecho de que posee una demostración geométrica tan simple como solo tener que dibujar cualquier triangulo y con un instrumento transbordador medir sus ángulos internos y sumarlos para notar que sin importar que triangulo dibujes, verás que la suma total es 180° .
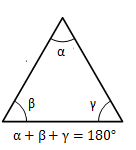
Fig. 1. La suma de los ángulos internos de un triángulo es igual a 180°.
Entonces pensé en poner a prueba esta demostración dibujando tantos triángulos como sea posible para medir sus ángulos internos, sumarlos y comprobar que en efecto, la suma total de sus ángulos sea 180 grados, sin embargo considero que no seria muy practico ya que eso dependeria de la cantidad de triángulos que pueda dibujar. Así que decidí realizarlo por otro modo y pense que podria realizar un script en MATLAB que "dibuje" los triángulos, haga las medidas de los ángulos y los sume para verificar que en cada caso su suma sea o no 180° grados.
El apoyo teórico en este caso es el teorema de coseno, el cual es una generalización del teorema de pitágoras y es usado para encontrar los lados de un triangulo cuando se conocen dos lados adyacentes y el angulo que forman estos o para determinar algún angulo interno desconocido conociendo el valor de los 3 lados que forman el triangulo.
Metodologia
Para hacer la simulación, definí los siguientes pasos:
- * Establecer una serie de longitudes aleatorias (3 para cada triángulo). Para ello, definí tres pares de puntos aleatorios que hicieran de coordenadas para los vertices del triangulo.
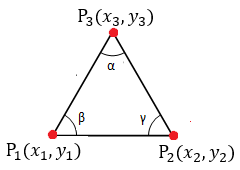
- * Definido dichos puntos, calculé las distancias entre ellos a través de la siguiente expresión
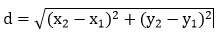
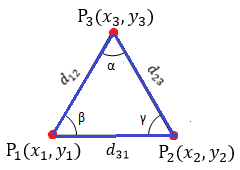
- * Calculados los lados de cada triangulo, utilicé el teorema del coseno para calcular los ángulos internos de cada triángulo definido en el paso 1. La ecuación que relaciona el ángulo desconocido con los lados del triangulo:
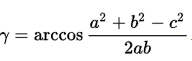
 ) es el angulo a calcular.
) es el angulo a calcular. - * Luego de haber calculado cada angulo sumé los ángulos obtenidos en el paso 2. y verifiqué si para cada triángulo, su suma sea efectivamente 180°.
- * Tras haber hecho los pasos anteriores, repeti el experimento usando otros valores aleatorios para las coordenadas de los vertices del triangulo.
o=0;
f=0;
for i=1:1000
%Puntos del triangulo definidos aleatoriamente
p1=10rand(1,2);
p2=10rand(1,2);
p3=10rand(1,2);
% Distancia entre los puntos
d12=p2-p1;
d23=p2-p3;
d13=p3-p1;
% Modulo de la distancia entre los puntos
a=sqrt(sum(d12.^2));
b=sqrt(sum(d23.^2));
c=sqrt(sum(d13.^2));
% Angulo "A"
an1=acos(((a)^2+(b)^2-(c)^2)/(2ab));
% Angulo "B"
an2=acos(((c)^2+(b)^2-(a)^2)/(2cb));
% Angulo "C"
an3=acos(((a)^2+(c)^2-(b)^2)/(2a*c));
suma=radtodeg(an1+an2+an3);
suma=round(real(suma));
if suma==180
o=o+1;
else
f=f+1;
end
end
disp('Hay una cantidad de aciertos de'), disp(o)
disp('Hay una cantidad de fallos de'), disp(f)
Resultados
10 Triangulos

50 Triangulos

100 Triángulos

1000 Triángulos

10000 Triángulos

que cosa más curiosa! Me encantó. Un beso para el escritor del post :* <3
gracias!
buen tema le recomendaria q subiera algo mas llamatio para que consiga llamar mas la atencion de las comunidades
Lo tendre en cuenta, gracias
Hola, estoy asombrada de la habilidad del manejo de editores. Felicitaciones.
muy bueno
Muchas gracias!
Gracias!
Hola también uso matlap, sobre todo para análisis matricial de estructuras...saludoss
Gracias amigo.
@OriginalWorks
The @OriginalWorks bot has determined this post by @williamsq to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
No soy muy amigo de las matematica, pero buen post.
Pero las matematicas son amigables, a veces jajaja