Over the last couple of years I have heard quite a lot about an interesting equation, well "law" actually, that has been used to attribute value to certain social communities.
It's been used to attribute appropriate values to Facebook, Google, Amazon, and more recently it has even been used to calculate an appropriate value for bitcoin.
What am I talking about you might ask?
I am talking about none other than Metcalfe's Law.
Metcalfe's Law states that the value of a system is proportional to it's number of users squared.
Specifically it's defined as:
"Metcalfe's Law states that the value of a telecommunications network is proportional to the square of the number of connected users of the system (n^2)"
The "law" was originally presented in 1980 but wasn't formulated in the above way until 1993 by Professor George Gilder.
The intent was to try and explain the network effect. How adding more users to a system doesn't just increase that network's value linearly but instead exponentially.
To illustrate that, the "law" is stating that if you have 100 users and a value of 10,000 and you double your user base to 200, the current value of your users doesn't double and go to 20,000. Instead it goes to 200^2 or 40,000.
Cool, but what's the big deal?
The reason I bring this up is because my favorite Analyst on the Street (Tom Lee) has been using this model for some time now to predict bitcoin prices.
Well perhaps, not so much predict, but to help get an idea of what plugging in certain numbers might do to prices of the coin.
Namely, expanding the number of users in the bitcoin network.
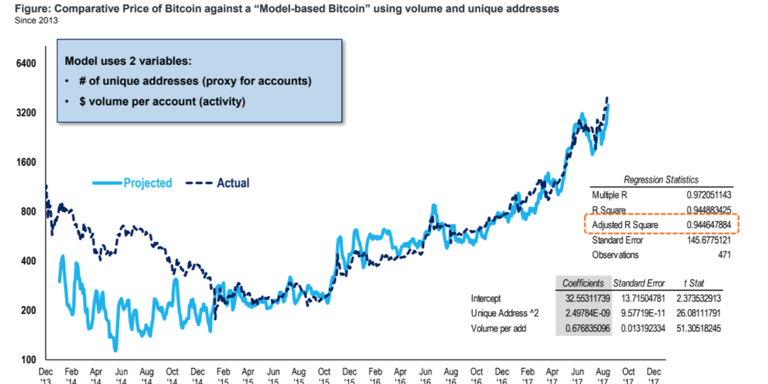
Surprisingly, (or not surprisingly), Lee's modeling has been extremely accurate!
Check it out:
Perhaps better than being a price predictor, this data might be useful indicating whether prices are in "bubble territory" and when prices are undervalued relative to their network usage.
For example, in the above model you can see that when the model was well below the actual line, the price eventually made it's way down to where the model was. Meaning that if you had looked at this at that time you might have guessed prices were a little overheated due to actual network usage.
Basically, this is saying that if you see a big divergence, in one direction or the other, between the number of active users squared and the price, perhaps you can gain some insight as to where prices might go next (if those usage numbers remain constant that is).
More on Tom Lee and his ideas behind using Metcalfe's Law in regards to bitcoin can be read here:
http://www.businessinsider.com/bitcoin-price-how-to-value-fundstrat-tom-lee-2017-10
Cool! How does this relate to steem?
I'm glad you asked!
For one, I would think that steem is probably even a better example of the network effect as its primary users mostly come from the social media site steemit.com.
Knowing that information, is it possible we could come up with a theoretical price of steem?
Maybe!
According to data pulled from @penguinpablo's daily steem stats report we can see that yesterday steemit.com had roughly 24,000 daily active users:
https://steemit.com/steemit/@penguinpablo/daily-steem-stats-report-friday-november-10-2017
(chart courtesy of @penguinpablo)
Applying Metcalfe's Law from above we can take that 24,000 active users number, square it, and come up with roughly 576,000,000 of value. (24,000 x 24,000)
That means with that number of active users, the total value of the system should theoretically be somewhere around $576,000,000.
More than double the current market value of $243,000,000.
To get a theoretical price of steem based on those numbers, we simply divide that 576,000,000 by the number of steem outstanding, which currently is 259,000,000.
(576,000,000/259,000,000)
Performing that calculation would give us a value of $2.22 per unit of steem.
Pretty cool eh?
Congratulations @ankitgoyal09! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP