
This is the first part of the guide, related to the basic concepts and the new curve introduced in the hardfork 21:
- Steem power and vests
- Reward shares
- Claims
- Convergent linear curve
- Payout distribution
Steem power and Vests
The steem power is the value of your vesting measured in steem. There is a common fund called total vesting fund steem (Fs), which contains all the steem that has been powered up, and each account has a part of it. The vesting shares (vs) determines how much steem of this fund your are entitled compared with the total vesting shares (VT).
Thus, the steem power is calculated as
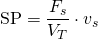
Actually, this relation (Fs/VT) is equal to 503 steem per million vesting shares and this value is almost constant over time. It has an annual interest calculated by:
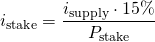
where isupply is the annual inflation of the virtual supply, and pstake is the percentage stake, which is the relation between the total vesting fund steem (Fs) and the virtual supply (Vsupply):
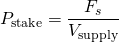
Today the percentage stake is 56% and the stake interest is 2.2% annual. The annual inflation of the virtual supply is 8.38% (which decreases 0.42% per year)
Reward shares (Rshares)
Each vesting share in the system has the right to generate, in a period of 5 days, 1 million rshares (positive or negative) plus 250k negative rshares. The generator is called the manabar, and the remaining rshares to be generated is called the current mana. The rshares are generated when voting and are transferred to the post.
As part of the hardfork 21 there are 2 manabars: The principal one for upvotes and downvotes (the one with 1 million rshares per vesting share), and the second one only for downvotes (250k negative rshares).
However, all rshares can not be generated in a single vote, but maximum 2% and 8% from the current mana of the principal manabar and downvote manabar respectively.
Note that the downvote manabar generates 1/4 of what the principal manabar generates, but at the same time it can be consume 4 times faster than the principal manabar. In the end, a single vote has maximum 2% of all posible rshares that can be generated with a certain amount of vesting shares.
Then, the rshares generated in a vote are:
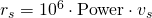
Where Power is a value between 0 and 0.02 and represents the percentage taken from the principal manabar, or the percentage taken from the downvote manabar divided by 4.
Considering that the relation between steem power and vesting shares is around 500 steem per million vesting share, and that a user is voting with his maximum power (0.02), then the rshares can be calculated as:

Threshold and last minute vote
There are 2 more rules regarding the rewards shares:
- Threshold. Always, no matter the value of the vote, 50 million rshares are subtracted from the rshares (and limited to 0 rshares). This is to prevent spamming. Using the previous formula we get that it represents a difference of 1.25 steem power, a very low value that can be neglected.
- Last minute vote. If the vote is done 12 hours before the payout then the reward shares are decreased proportionally to the remaining time for the payout. That is, half before 6 hours, and 0 just at time of the payout.
Claims
Claims represents the shares in the reward pool. Each 3 seconds, 65% of the new steem generated is transferred to the reward pool (called reward balance, RB). And this amount is compared with the total claims (called recent claims, RC) from all posts of the last 15 days. Each post has entitled some amount of claims, which depends on the number of rshares obtained. Then the post payout, measured in steem, is
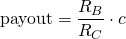
where c is the number of claims.
Reward balance and the recent claims are 2 values that are constantly changing, and depend on the activity of authors and curators. Let's try to figure out an approximation.
Suppose that the activity of authors and curators is constant, meaning that new claims are compensated with the removed claims. If this is true then reward balance is equal to the new steem generated for rewards during 15 days, that is:
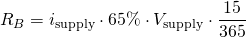
On the other hand, we know that 1 vesting share has the right to generate 1 million rshares in 5 days. Then, in 15 days it can generate 3 million rshares. Let's define Pactive as the percentage of steem power from all accounts that is used actively used in curation. Then the rshares generated in the last 15 days (recent rshares RR) are
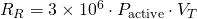
In the harfork 19 and 20, this calculation is equal to recent claims, because one claim is one rshare.
So it is easy to calculate the active percentage in the hardforks 19 and 20 using this formula. Currently is around 50%.
But the problem is that in the hardfork 21 claims and rshares are different. Let's define "claims per rshare" (CR) as the average of claims that are generated per rshare. As we will see later, this value is between 0 and 1, and it is related to the distribution of votes (popular and non popular content). A value near to 0 means that there are a lot of posts with low votes and few with high votes. And the contrary with 1, a lot of posts well voted and few posts with low votes.
I performed a data analysis and today claims per rshare would be equal to 0.9 assuming we were in the hardfork 21.
Then, the recent claims can be calculated as
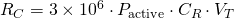
Taking the previous calculations, and also the percentage stake, we get that the relation between reward balance and recent claims is

If we suppose that most of these values remain constant (503 steem per million vests, 8.38% annual inflation, 56% percentage stake) then

This formula summarizes something evident but important to mention:
- As long as more steem power is used (more Pactive) the payments will decrease because the same reward is distributed to more hands.
- Each claim has more value when claims per rshare is low. Meaning that good posts have better return than the average compared with the linear rewards of HF19 and HF20.
Convergent linear curve
During the hardforks 19 and 20, one rshare was exactly one claim. The reason they are called "linear rewards" is because the claims are proportional to the rshares (1 to 1), and as the rshares are proportional to the steem power then a vote has the same value no matter if a new or popular post is voted.
However, the hardfork 21 introduces a new curve which is non linear, called the convergent linear curve. Its name is because it starts being a quadratic curve but as long as there are more rshares it tends to the linear curve. In this curve, the claims are calculated as
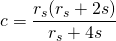
where rs are the rshares obtained by the post, and
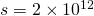
Derivative of claims
You maybe wondering what is the value of a vote in terms of steem or sbd. The answer is that it depends on the post you are voting. When a post receives a new vote it increases its total rshares, and this growth represents an increase in the claims.
The derivative of the curve tells us how much is the growth of claims with respect to the growth of rshares.
The derivative of claims is

- This derivative evaluated in infinity gives 1, meaning that 10 rshares give 10 claims to the post if it was already popular (a lot of rshares).
- This derivative evaluated in 0 is equal to 1/2, meaning that 10 rshares give 5 claims to the post if it is new (no previous rshares).
As you see, there is a factor of 2 between voting a new post or a popular post. But what means infinity? at which point we can consider that the derivative is 1? To answer that let's see the inverse function of the derivative:
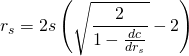
At which point the derivative is 0.9? in other words, if I vote with 100 rshares and it adds 90 claims to the post, what was the total payout of the post?
The answer is 9.89 Trillion rshares, which are the rshares that an account with 247K SP can give in a single vote. So, at this point we can say that the curve is almost linear.
The following table shows more values for the derivative and the expected rshares to reach it.
| Derivative | rshares | claims | Payout* |
|---|---|---|---|
| 0.8 | 4.65e+12 | 3.18e+12 | 4.5 steem |
| 0.9 | 9.89e+12 | 7.68e+12 | 11 steem |
| 0.99 | 4.86e+13 | 4.51e+13 | 64 steem |
| 0.999 | 1.71e+14 | 1.67e+14 | 238 steem |
- The payout value assuming that active percentage is 50% and claims per rshare is 0.9
The gap
Let's define clineal as if the claims were calculated in linear rewards, and payoutlineal as if the payout were calculated using clineal:
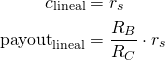
Now, let's rewrite the formula for claims. The idea is to see what is the difference between the payout and the linear payout. After some calculations it is easy to get:

If we evaluate this formula in infinity (popular content) we get that:
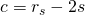
Meaning that claims are almost proportional to rshares, to the steem power. If the post is popular then we just have to subtract 2s from the rshares to calculate the claims.
This difference of 2s is what I call the gap. If we multiply the formula by RB/RC we get the relation seen in terms of steem:
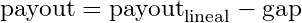
being the gap equal to
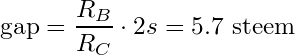
This formula is very important, because is telling us that the payout can be calculated as the linear payout minus 5.7 steem* in popular posts.
- This value assuming all the constants calculated in the first part of the post.
If the post is not popular, the amount subtracted is less than the gap. In general, the payout is:
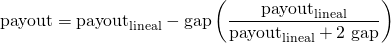
Self voting farm
Suppose that an account is creating k1 posts daily for self votes. Also, suppose that the account can create a total of X rshares daily. This means that to maximize the returns he is giving X/k1 rshares to each post. What is the payout he is getting?
Supposing that the posts are greater than 40 steem, we can consider they breach the gap and the rewards are almost linear. Being c1 the claims obtained per post then:

Now suppose that he changed the strategy to k2 posts daily. In this case:
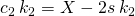
What is the difference of these 2 strategies in terms of claims?
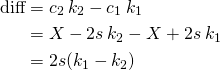
Which in terms of steem represents a difference of
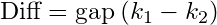
Let's see some examples:
- Suppose that an account is making 60 posts daily. How can he maximize profits? If instead of dividing the steem power between 60 posts it is divided by 10 posts daily, then the account will get 285 more steem daily.
- Suppose that a guy has 4 accounts and each account creates 20 posts daily. How to maximize profits? If all the steem power is concentrated in only 10 posts of one account, then the extra profits are 5.7(80-10) = 400 steem daily.
Note that in these examples we do not mention what is the payout of each post. The unique assumption was that they were big. However we can calculate the extra profits.
Another way to understand this concept is using the analogy of taxis. When you take a taxi you pay a basic fare and on top of that the price of the distance to the final destination. But what happens if this distance is divided in two travels and you take two taxis? you pay two times the basic fare to travel the same distance. Here is the same with the gap, no matter the distance (rshares), what really matters when reducing costs is the number of times you take a taxi (number of posts) and pay the basic fare (gap).
As conclusion, the concentration of power in few posts will have better return than the distribution of power. However, as it is more concentrated then is more visible and discoverable for the community, which can downvote them if it is poor content. This is the principal objective of the convergent linear curve, the concentration of power.
This difference in profits is for the specific case when the payout is much greater than the gap and it can be considered to be in the linear zone. However, if it is not, then a more generic difference can be calculated as:
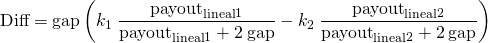
Bidbots
We saw before that the value of the vote depends not only on the rshares but also on the previous votes to the post. Then, regarding to bidbots, is difficult to measure what is the actual return for a particular bid. The relation 1:1 between rshares and claims is not valid anymore.
For this reason I think bidbot owners will calculate the vote using rshares as reference and not claims. In this scenario the payoutlineal will be proportional to the bid:
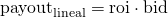
Then

Again, let's see a similar calculation to the previous section. Suppose that X amount of money is used to promots k1 posts. Then the payout is
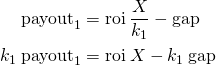
If instead of k1 posts this money is distributed between k2 posts then

And the difference between these two strategies is
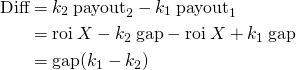
Example: A bid of 7 times 100 steem will get 34 more steem than 7 bids of 100 steem to different posts. And the conclusion is the same: There are more returns if the power (and bids) are concentrated in few posts.
Payout distribution
The hardfork 21 introduces a new change in the payout distribution. Now, 50% of the payout goes to the author and 50% goes to curators.

All payments for curators are powered up and transferred as vesting shares. In the case of the author, he can decide how much is payed as steem power and how much as SBD, with maximum 50% for SBD.
At the same time, the author can decide to distribute the payment among previously defined beneficiaries. The relation steem power / SBD is kept the same in this case.
The conversion from steem to SBD is done using the median feed price defined by the witnesses. Some rules are implemented in order to prevent the excessive debt and hyperinflation. They are described with the following concepts:
Debt ratio. This ratio is defined as the percentage of the SBD supply (converted to steem) with respect the virtual supply. It is expected that this value does not exceed 10%.
SBD print rate. When the debt ration is between 9% to 10%, then the SBD print rate varies from 100% to 0%. In this case, the author will receive part in SBD and part in steem depending on the amount that was converted.
Haircut. If the debt ratio reach 10%, meaning that the steem price is very low, then the peg to the dollar is broken and the haircut price is used for all conversions. This new price is exactly 9 times the sbd supply divided by the steem supply, which does not let the debt ratio increase beyond 10%.
This guide continues and finishes in the second part where we discuss the distribution of curation rewards.
Stupid question: if someone were to do two 100% downvotes per day, would the manabar with 1M rshares per vesting share remain unaffected?
You can cast a 100% upvote every 2.4 hours to get maximum effectiveness.
With HF21, you will be able to cast a 100% downvote every 9.6 hours for maximum effectiveness without effecting your upvote manabar.
Interestingly, if you keep your upvote manabar at max, I think you can do like 12 "full power" downvotes at the same time, which just about exhausts the downvote manabar completely. At which time you can wait for the downvote manabar to go back or dip into the main bar.
Ah right, because the whole thing is based on votes (actually recharge) per five days, when we usually think of it in votes per day terms. Good point.
Yes, you are right. To be exact it is 12.5 full power downvotes.
Remain unaffected. As netuoso said you will be able to cast a 100% downvote every 9.6 hours.
Then you can make 5 downvotes (100%) in 2 days without affecting the principal manabar.
I'm confused about this:
I thought the "last-minute" window was 12 hours, right now, and this wasn't going to change with HF21?!
There is however a 5 minute window with reduced curation rewards right after the post has been made.
Did something get mixed up here or is the "last-minute" really being decreased to 5 minutes?!
P.S.: I checked on github
it's a bit confusing still as it's indeed defined as 5 minutes earlier in the same file, but I'd assume that's a testnet-only setting and the later definition overwrites that.
From HF17 to HF19 the window was 12 hours.
But it was changed in the Hardfork 20. Now it is 5 minutes.
https://github.com/steemit/steem/blob/bdf0fb51361c26537428efcd9a65433ffe09abbf/libraries/chain/steem_evaluator.cpp#L1958-L1961
which is set to 12 hours according to the definition posted above (edited for clarity)?!
https://github.com/steemit/steem/blob/v0.21.0/libraries/protocol/include/steem/protocol/config.hpp#L61-L62
Ohh I see. I was looking the value for testnet. You are right, it is 12 hours. I will change it. Thanks.
No worries, I wasn't 100% sure myself until I actually looked into the code.
Either way, your posts on the matter help me greatly with wrapping my head around the new rewards.
Thanks for taking the time to put this all together!
!SHADE 2
Thanks for sharing on Pimp Your Post Thursday
Stephen Hawking was told that every equation in his books would lose him half his readers (I think). By that maths I should think about 3 people read this to the end. I think people just want to know if they will make anything if they do not have whale support. If you are a minnow then extra curation rewards will not make much difference.
Thanks @steevc. I appreciate your comment, you are right.
My intention with this post is to fill a hole in the system: Detailed documentation of how it works.
I think it's unacceptable that if you want to know how it works in detail you not only have to be a software developer but also take the time and be patient to read the code, which is very difficult from the beginning.
In physics you have a lot of books explaining everything in detail. Then you can write a book without formulas to reach many more people. But here in steem is the contrary.
For future readers, these posts can also be useful to get a description of the general idea:
Unfortunately a lot of the explanations of how Steem works are too technical for the average person. I appreciate what you are doing, but I hope others can give a simpler version. I'm a developer and a lot of it goes over my head. We just want to know how it affects us.
I don't care if I am one of the three - this level of knowledge is necessary as I have zero faith in the words that are used to promote changes that are deeply mathematical and that may well need different words to truly explain them.
"My intention with this post is to fill a hole in the system: Detailed documentation of how it works."
Absolutely and thank you! We need to know the maths, not just the BS. I wrote on this too but was less than positive.
The next level above the encoded mathematics is how it will play out as game theory :-)
The curation curve is a joy of instability! I'll read your part 2.
Have fun everybody
Posted using Partiko Android
I'm a little confused about the non-linear thing.
Can I just check if my understanding is right?
Currently, if you receive x rshares on your post, it doesn't matter if this came from one big vote of lots of small ones, it's just the total rshares added up that is the post payment.
However, if we go to non-linear and the total rshares of x came from several voters rather than just 1 voter, the post earns more?
It doesn't matter if "x" rshares come from several voters or just 1 voter, these x rshares are added to the post, and the payout will be the same.
The difference is in the amount of rshares.
Currently (HF20):
The payout for 10^9 rshares is 1000 times the payout for 10^6 rshares.
The payout for 10^12 rshares is 1000 times the payout for 10^9 rshares.
The payout for 10^15 rshares is 1000 times the payout for 10^12 rshares.
The payout for 10^18 rshares is 1000 times the payout for 10^15 rshares.
The payout for 10^21 rshares is 1000 times the payout for 10^18 rshares.
However, with the new curve (HF21):
The payout for 10^9 rshares is 1000 times the payout for 10^6 rshares.
The payout for 10^12 rshares is 1111 times the payout for 10^9 rshares.
The payout for 10^15 rshares is 1793 times the payout for 10^12 rshares.
The payout for 10^18 rshares is 1004 times the payout for 10^15 rshares.
The payout for 10^21 rshares is 1000 times the payout for 10^18 rshares.
Wow just wow... No 50/50....
Posted using Partiko Android
thank you for this explanation.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Please consider using the steemstem.io app to get a stronger support.
Hi @jga!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 4.647 which ranks you at #1761 across all Steem accounts.
Your rank has improved 75 places in the last three days (old rank 1836).
In our last Algorithmic Curation Round, consisting of 366 contributions, your post is ranked at #144.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
@jga little bit confusing and little bit happy. This is my current situation. :-(
totally out of mind..🙄
Posted using Partiko Android
Thanks, this is the right level of mathematics needed :-)
Sorry I hadn't seen this before.
One question: why do recent steemitblog posts mention 20 STEEM as a kind of pivot point for earning more/less between HF20 and HF21?
the last time I looked on github, the chosen reward curve parameter was 2e11. has that been changed?
I see you use 2e12.
Maybe the quoted 20 STEEM is not quite the pivot point.
Would appreciate a reply. Thanks.
Sorry, posted from wrong account - happens.
But, yes, which reward curve parameter has been finally chosen?
And where did the 20 STEEM reward pivot point come from? It was either 4 or 6 STEEM for 2e11 and 2e12 respectively.
Thanks
Thanks was super useful for me, thank you! !tip 5 steem
Thank you very much cardboard!
🎁 Hi @jga! You have received 5.0 STEEM tip from @cardboard!
Check out @cardboard blog here and follow if you like the content :)
Sending tips with @tipU - how to guide :)