ATOMIC THEORY: Activity and Half-life

The activity of a radioactive source is the number of ionizing particles it emits per second. Each emission corresponds to a change in the nucleus of one atom and is also called the decay rate. The SI unit of activity (and decay rate) is the becquerel (Bq):

1 Bq = 1 decay per second

What we actually record is the reading on any radiation detector we use to monitor the effect of the radiation. Usually, this is the count rate as measured by a Geiger counter. The count rate is simply the number of counts recorded per second, and in simple experiments, it is taken to be directly proportional to the activity. Note that it is very unlikely that all the decays of a source will be recorded. Usually, some of the radiation is trapped inside the source, and in most measurements, only a small fraction of the radiations actually enter the detector to be counted.

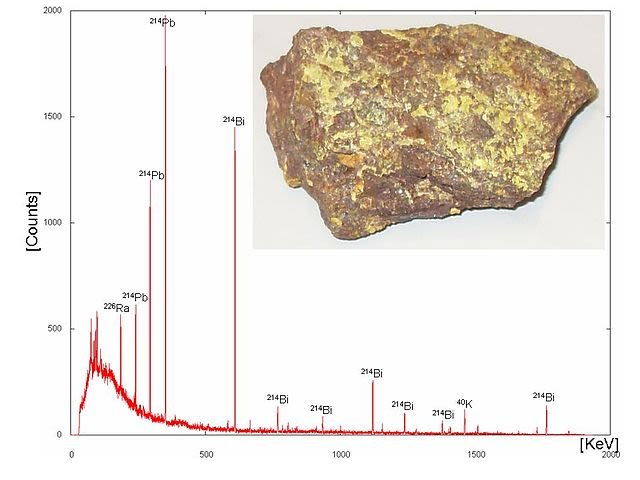
^{Gamma-ray energy spectrum. Wusel007, CC BY-SA 3.0}

As time goes on, the activity of a source (and so the count rate) decreases in a consistent manner. There is a typical plot of the alpha particle count rate against time for a small sample of the radioactive gas radon (Rn-220).

The graph has been drawn as a ‘best fit’ through actual numbers recorded by a counter. The count rate in counts per second is calculated from the number of counts measured at 10-second intervals. There are two significant features of the graph. One is that the values aren’t all on the line, so the measurements have some inbuilt uncertainty. Secondly, as the annotation shows, the time taken for the count rate to fall from 400 s^-1 to 200 s^-1 is the same as the time for the count rate to fall from 200 s^-1 to 100 s^-1. That is, the graph suggests that:

The time taken for the activity of a radioactive sample to decrease to a half of any starting value is the same, whatever the starting value of the count rate.

This time is called the half-life of the radioactive substance.

RANDOMNESS OF DECAY

Both the uncertainty in measuring and the constancy of the half-life have the same cause: the time at which any given radioactive nucleus emits its radiation cannot be predicted. It is impossible to tell which one of a hundred radon nuclei will be next to emit its alpha particle. All the nuclei are identical, and all are equally liable to decay. But the breakdowns are completely random. However, if we have a sample of several hundred billion radon nuclei, a pattern would emerge. Bear in mind that ten billion (10¹⁰) radon nuclei have a mass of a few thousandths of a billionth of a gram (about 4 × 10^-12 g).

What is constant about the radioactive process is that each nucleus has a definite probability of undergoing decay. Starting with a large enough number of radon nuclei, we can be reasonably certain that a predictable number will emit an alpha particle in the next 10 seconds. Similarly, with a large enough sample, the values of count rate we measure will coincide closely with the smooth graph we draw between the values. Our estimate of half-life will be more reliable.

THE SHAPE OF THE ACTIVITY CURVE

We associate an exponential change with any system where the change is proportional to the quantity that is changing, either increasing or decreasing. An example of an increase is a biological population growth, where the number of young born is proportional to the number of organisms in the population. This property is also characteristic of many physical changes. The graph plotted above is a decay curve for an exponential change to a radioactive material, and here the decrease in the population of nuclei is exponential: the decay rate decreases by equal fractions in equal times. The fraction that we use for a radioactive material is a half, so we refer to its half-life.

Mathematically, if ΔN is the number of nuclei that decay in a small time Δt, then:

ΔN = -KNΔt                                         [1]

The minus sign is because ΔN is a reduction in N: as time goes on N decreases. The decay constant k is a measure of the probability of a nucleus decaying in the following second. (Each radioactive nucleus has its own value of k.)

The passage overleaf gives the calculus version of deriving the exponential form of radioactive decay.

THE DECAY CONSTANT AND HALF-LIFE

For a radioactive nucleus, the decay constant indicates the probability that the nucleus will undergo decay. Its value is in terms of the fraction of the potentially active nuclei in a sample that do actually decay in any second of time. So, the larger the value of k, the higher the number of nuclei decaying in a given time and the shorter the half-life. The passage below shows that the relation between half-life and the decay constant is:

half-life (in seconds) = ln2 / k                      [2]

Where In 2 is the logarithm to base e of 2 (0.693).

EXAMPLE

Question: The half-life of bismuth (Bi-212) is 60.6 minutes. What is its (a) decay constant, (b) the activity of 1 g of bismuth-212? Taking the Avogadro constant as 6.02 × 10²³.

Answer: (a) Half-life of bismuth = (ln 2)/k,

So, decay constant k = 0.693/(60.6 × 60) = 1.91 × 10^-4 s

(b) 212 g of bismuth-212 contains 6.02 × 10²³ atoms.

Therefore number of atoms in 1 g:

N = (6.02 × 10²³)/212 = 2.84 × 10²¹

The probability of decay for bismuth-212 is k per second. Thus we would expect kN atoms to decay per second:

activity kN = 1.91 × 10^-4 × 2.84 × 10²¹ Bq = 5.4 × 10¹⁷ Bq

^{Half-life demonstrated using dice in a classroom experiment. 13hartc, CC BY-SA 4.0}

THE ATOMIC NUCLEUS

Atoms are mostly empty space. We picture a hydrogen atom, as a very small central blob of matter surrounded by a single rapidly moving electron. The central nucleus contains 99.95 percent of the atom’s mass but only a ten-billionth part of its volume. The space surrounding the nucleus is occupied by the single electron, moving so rapidly that we can think of it as being everywhere in the space at once.

THE VERY FIRST NUCLEAR PROBE – ALPHA SCATTERING

The first evidence for the existence of the nucleus was the alpha scattering experiment of Geiger and Marsden in 1909 at the University of Manchester under the leadership of Ernest Rutherford. At that time, most physicists’ idea of an atom was of a round ball completely filled with a positive ‘jelly’ in which the newly discovered electrons were embedded, like currants in a currant bun. Rutherford told his assistants, the experienced Hans Geiger and a young undergraduate, Ernest Marsden, ‘See if some effect of alpha particles directly reflected from a metal surface.’ A diagram of the apparatus they used is shown in the figure below. It shows the main features of all such collision or scattering experiments:

• a source of high-speed particles,
• a vacuum to avoid unwanted collisions.
• a target, or more precisely the atomic or subatomic components of the target,
• a detector of the scattered particles or any fragments produced,
• a means of measuring the paths of scattered particles or fragments.

A radioactive source, contained in a lead box with a small hole in it, emitted alpha particles. The targets included thin gold foil only a few atoms thick. Most alpha particles went straight through the foil, and were detected by the faint glow (scintillation) that each particle produced when it hit a detecting glass screen coated with a phosphorescent chemical. The scintillations were so faint that Geiger and Marsden had to allow half an hour before each observation session for their eyes to become ‘dark adapted’.

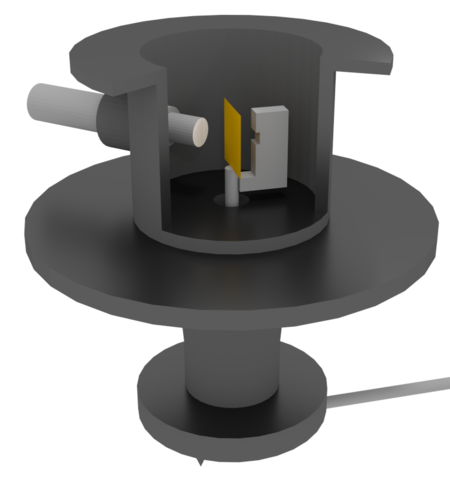
The detecting screen was fitted to a pivoted arm moved along a scale marked in degrees. About one alpha particle in 8000 was reflected back through a large angle. An alpha particle is deflected by repulsion from another positively charged object. The ‘positive jelly’ model proposed by J.J. Thomson  would have provided a repulsion force far too small to deflect the massive alpha particle through a large angle – it predicted a deflection of 2° at most.

Rutherford deduced that there must be a very much stronger electric field inside an atom, which could only be produced by a very high charge density, such as if all the charge were locked into one small volume. For the fast and quite massive alpha particle to bounce back at all, most of the mass of the atom would also have to be squashed into this small space. Rutherford named this small space, in which all the positive charge and most of the mass of an atom is concentrated, the atomic nucleus. By comparison, the electrons had negligible mass but occupied most of the space.

In the illustration of Rutherford’s idea of what was happening in the gold foil experiment. Alpha particle A passing some distance from the nucleus is hardly deflected at all – the electric field is too small. A closer approach such as B’s produces a larger deflection. A (rare) head-on ‘collision’, C, stops the alpha particle dead in its tracks and repels it back along its own path.

Rutherford wasn’t very keen on mathematics, and it took him nearly two years to produce a calculation which related his nuclear model of the atom to the distribution of the number of deflected particles and the angles they were deflected through.

Particle accelerators

Early experiments used naturally energetic particles to probe the nucleus, but by the 1920s physicists were using ‘atom-smashing machines’ to accelerate charged particles in a controlled manner. Their main techniques are still used today, though with greatly increased energies. One technique accelerates charged particles in a straight line by applying an electric field – a linear accelerator. The other uses a combination of electric and magnetic fields to accelerate the charged particles in a circular path – leading to such devices as ‘cyclotrons’ and synchrotrons.

NUCLEAR PATTERNS

Practically all the mass of an atom is the mass of its nucleus, which consists of particles called nucleons. There are two kinds of nucleon with very slightly different masses. The proton is electrically charged: its positive charge is equal in size to the charge on an electron. It is slightly less massive than its partner, the uncharged nucleon called the neutron. The Periodic Table of the chemical elements arranges the elements in the order of the number of protons in the nucleus, This number is the proton number or the atomic number, symbol Z. Adding the number of protons and neutrons gives the mass number or nucleon number of an element, symbol A.

Nuclides

The word nuclide is the name for atoms that have identical nuclei; this means they have the same proton number (atomic number) and the same mass number, so they have the same number of neutrons. Compare this with 'isotopes’ whose nuclei have the same proton number but different mass numbers (because they have different numbers of neutrons).

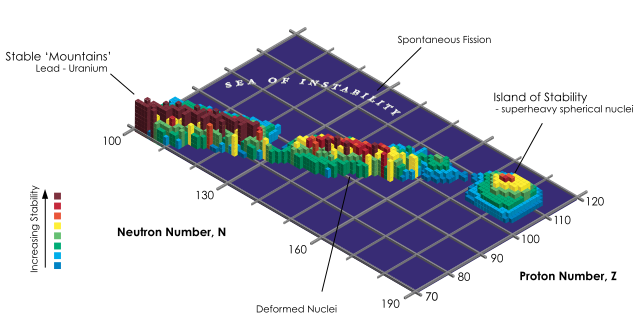
^{Stability of nuclides. InvaderXan, CC BY-SA 3.0}

REFERENCES

http://physicsnet.co.uk/a-level-physics-as-a2/radioactivity/radioactive-decay/ 

https://www.nde-ed.org/EducationResources/CommunityCollege/RadiationSafety/theory/activity.htm 

https://physics.stackexchange.com/questions/177872/true-randomness-via-radioactive-decay 

https://en.wikipedia.org/wiki/Radioactive_decay 

https://isaacphysics.org/concepts/cp_radioactive_decay 

https://www.researchgate.net/figure/pH-optimum-curve-for-the-activity-of-an-enzyme-black-The-pH-of-the-maximum-is-the-pH_fig1_262878875 

http://physicsnet.co.uk/a-level-physics-as-a2/radioactivity/radioactive-decay/ 

http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/halfli2.html 

https://www.britannica.com/science/decay-constant 

http://www.chemistryexplained.com/Ar-Bo/Atomic-Nucleus.html

https://en.wikipedia.org/wiki/Atomic_nucleus

https://study.com/academy/lesson/atomic-nucleus-definition-structure-size.html

https://www.britannica.com/science/atom/Rutherfords-nuclear-model

https://socratic.org/questions/who-were-hans-geiger-and-ernest-marsden

https://en.wikipedia.org/wiki/Geiger%E2%80%93Marsden_experiment

https://en.wikipedia.org/wiki/Ernest_Marsden

https://www.britannica.com/science/alpha-particle

https://en.wikipedia.org/wiki/Discovery_of_the_neutron

https://en.wikipedia.org/wiki/Rutherford_model