"Del enunciado a la solución: 10 ejercicios de Ecuaciones Diferenciales de Variables Separables desglosados"

En el presente artículo, nos sumergiremos en el fascinante mundo de las Ecuaciones Diferenciales de Variables Separables, explorando diez (10) ejemplos cuidadosamente seleccionados de diversos autores reconocidos en el campo (las referencias completas se encuentran al final del artículo). Resolver una Ecuación Diferencial es una tarea fundamental en el cálculo avanzado y la física matemática. En esencia, consiste en una operación matemática cuyo objetivo principal es encontrar una función que satisfaga las condiciones establecidas por la Ecuación Diferencial en cuestión. Este proceso no solo es crucial para la comprensión teórica de fenómenos complejos, sino que también tiene aplicaciones prácticas en campos tan diversos como la ingeniería, la economía y las ciencias naturales.

El método de variables separables es una de las técnicas más poderosas y ampliamente utilizadas para resolver ciertos tipos de Ecuaciones Diferenciales. Este enfoque se aplica a ecuaciones que pueden reescribirse de forma que todas las variables dependientes estén en un lado de la ecuación, y todas las variables independientes en el otro.
A lo largo de este artículo, exploraremos diez ejemplos que ilustran la versatilidad y el poder de este método. Cada ejemplo ha sido seleccionado no solo por su valor didáctico, sino también por su relevancia en aplicaciones del mundo real.
Así pues, sin más preámbulos, adentrémonos en el fascinante mundo de las Ecuaciones Diferenciales de Variables Separables y descubramos cómo este método elegante y poderoso nos permite desentrañar algunos de los misterios matemáticos que gobiernan nuestro universo.

B I B L I O G R A F I A1.- A. Kiseliov, M. Krasnov y G. Makarenko. Problemas de Ecuaciones Diferenciales Ordinarias. Editorial MIR, 1984.
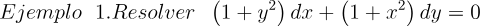
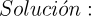
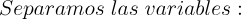
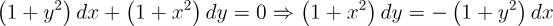
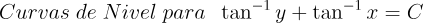
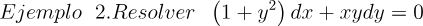
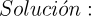
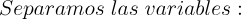
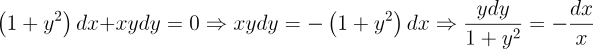
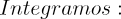
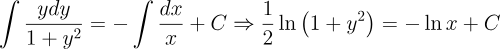
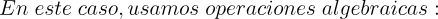
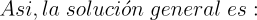
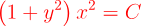
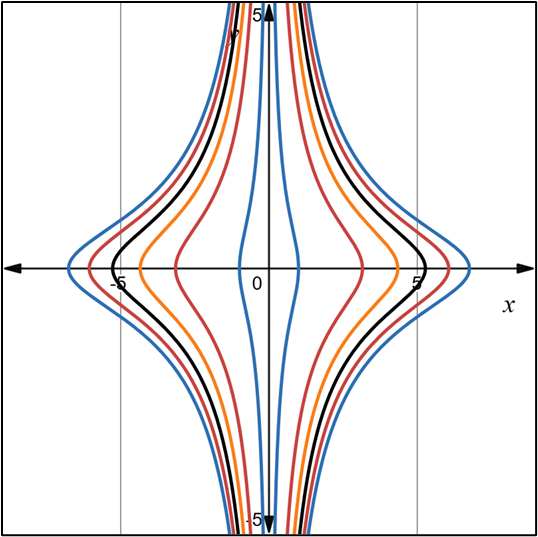
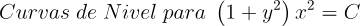
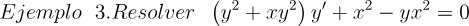
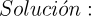
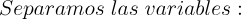
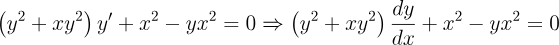
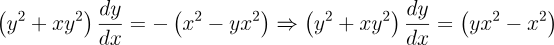
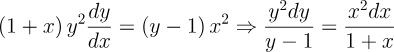
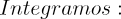
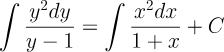
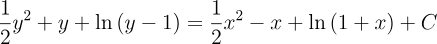
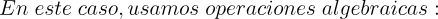
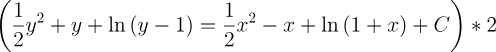
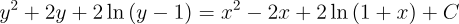
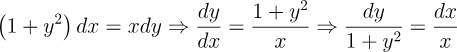
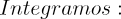
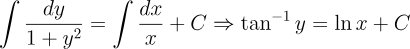
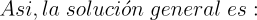
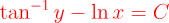
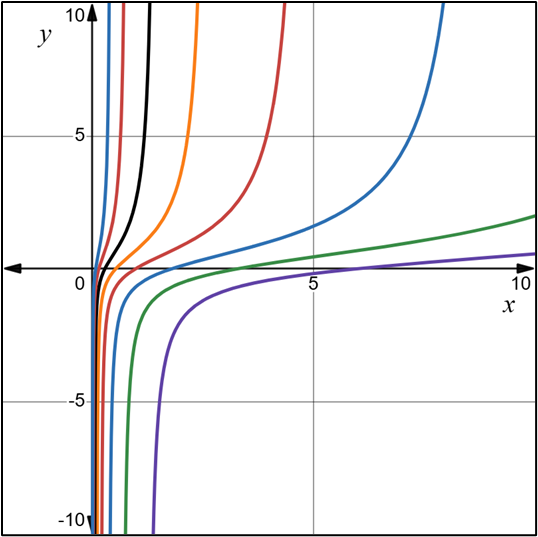
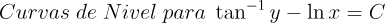
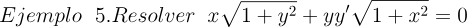
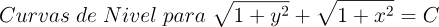
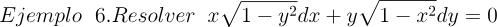
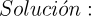
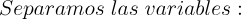
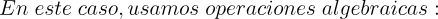
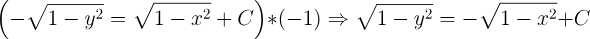
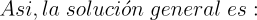
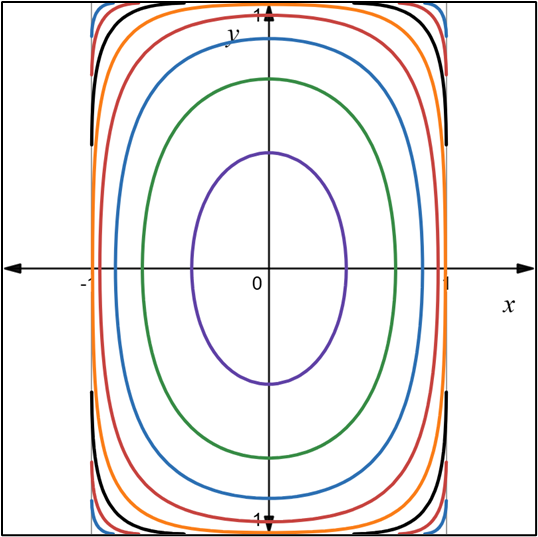
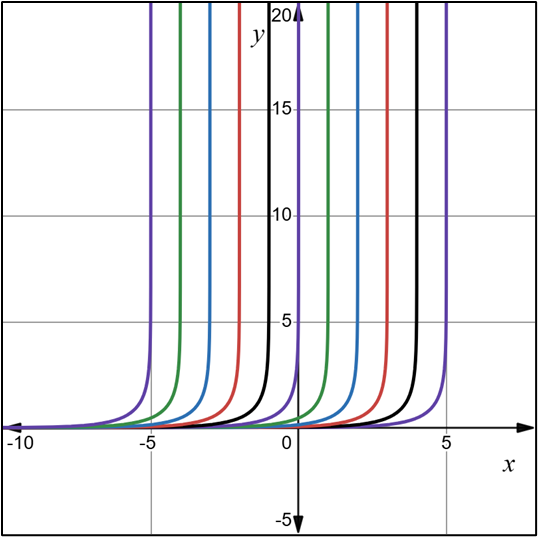
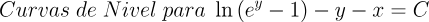
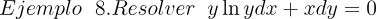
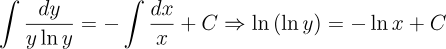
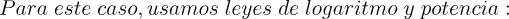
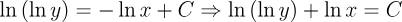
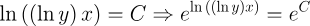
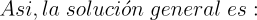
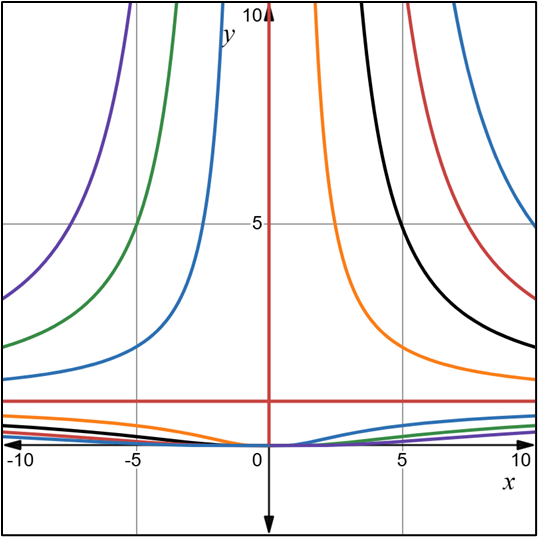
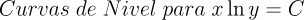
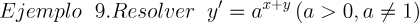
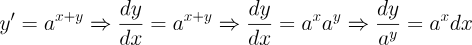
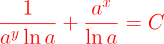
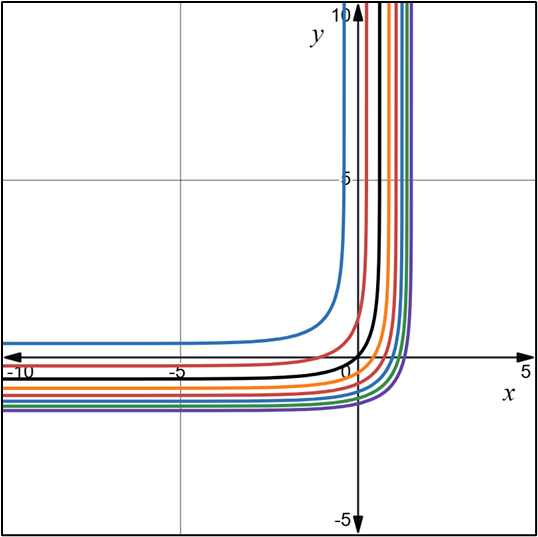
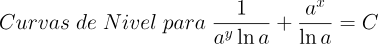
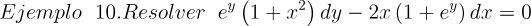
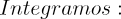
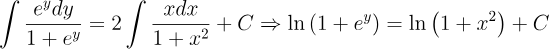
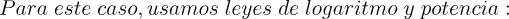
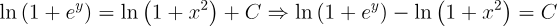
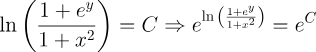
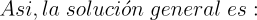
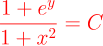
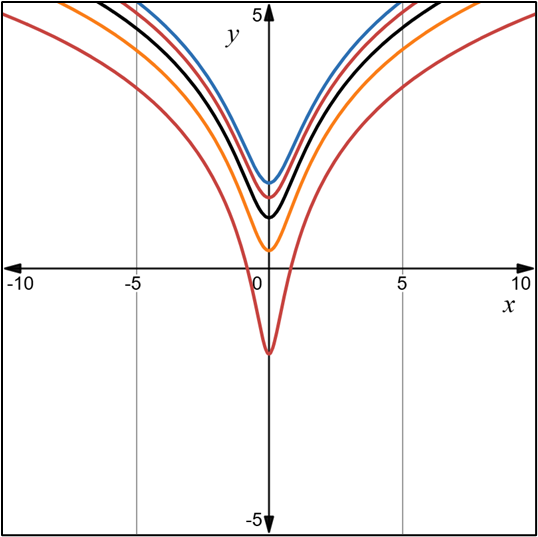
2.- Acero, Ignacio. Ecuaciones Diferenciales Teoría y Problemas. Editorial Tébar, 2007.
3.- Boyce, William E., DiPrima, Richard C., Meade, Douglas B. Ecuaciones Diferenciales Elementales y Problemas de Valores en la Frontera. Editorial Wiley, 2012.
4.- C. Henry Edwards, David E. Penny. Ecuaciones Diferenciales. Editorial Pearson Educación de México, 2001.
5.- Earl D. Rainville, Phillip E. Bedient, Richard E. Bedient. Ecuaciones Diferenciales. Editorial Pearson Educación, 1997.
6.- G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogany, G. Lunts, E. Porshneva, E. Sichova, S. Frolov, R. Shostak y A. Yanpolskí. Problemas y Ejercicios de Análisis Matemático. Editorial MIR, 1967.
7.- Jiménez López, Víctor. Ecuaciones Diferenciales: cómo aprenderlas, cómo enseñarlas. EDITUM, 2000.
8.- Larson, Robert P. Hostetler, Roland E. Cálculo y Geometría Analítica. Volumen 2. McGraw Hill, 1995.
9.- Morris Tenenbaum, Harry Pollard. Ecuaciones Diferenciales Ordinarias. Editorial Dover, 1963.
10.- Quintana, Pedro, Villalobos Eloísa, Cornejo María. Métodos de Solución de Ecuaciones Diferenciales y Aplicaciones. Editorial Reverte, 2008.
11.- R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y Problemas con Valores en la Frontera. Editorial Pearson Educación de México, 2005.
12.- Shepley L. Ross. Ecuaciones Diferenciales. Editorial Reverté, 1992.
13.- Zill, Dennis G. Ecuaciones Diferenciales con Aplicaciones. Grupo Editorial Iberoamérica, 1988.

Fuente de las imágenes.Las gráficas para las curvas de nivel se construyeron usando la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.