Antes de todo, reciban de mi parte, un muy cordial y afectuoso saludo para todos ustedes mis estimados Steemians-Lectores, para toda la comunidad de #stem-espanol, #steemstem y el resto de la numerosa comunidad de Steemit. Como ya muchos Steemians se han enterado a través de mis publicaciones es este medio, suelo presentar posts donde intento hacer que los conceptos básicos de la Física en distintas de sus áreas sean, clara y sencillamente, bien entendidos; lo cual es enormemente importante, como suelo decirle a mis víctimas (así llamo cariñosamente a mis estudiantes), ya que si se tienen bien entendidos los conceptos básicos, entonces se entenderán con mayor claridad las teorías más complejas donde estos estén involucrados. En este post sigo evolucionando en la elaboración de mis propios gifs animados ¡espero que los disfruten!.
El post que les presento en esta oportunidad, mis atentos Steemians-Lectores, se trata sobre las LIGADURAS (constraints en inglés). Las ligaduras las estudiamos y empleamos en la carrera de Física cuando cursamos Mecánica Clásica. Su correcto entendimiento, determinación y empleo es de vital importancia al momento de estudiar la Mecánica Lagrangiana que fue introducida por el Matemático, Físico y Astrónomo (francés e italiano) Joseph Louis Lagrange (1736 - 1813) en 1788 (ver figura 1 - Izquierda) y la Mecánica Hamiltoniana que recibe su nombre del Matemático, Físico, Astrónomo y Filósofo irlandés Sir William Rowan Hamilton (1805 - 1865) (ver figura 1 - Derecha); las cuales son teorías equivalentes a la Mecánica Vectorial de Newton, pero desarrolladas a partir de fundamentos energéticos.
Mis estimados Steemians-Lectores, como algunos lo saben, la Mecánica Clásica es uno de los cursos pilares en la formación de todo futuro Físico y es un curso avanzado de la carrera, por lo que las ligaduras suelen ser estudiadas en este nivel.
Sin embargo, en el presente post, les presentaré las ligaduras de una forma tan sencilla que pueden ser estudiadas a nivel de un curso básico de Física General, sin ningún problema, lo cual sería una ventaja a la hora de estudiar Mecánica Clásica más adelante en la carrera. |
|---|
Se requerirá sólo de conocimientos básicos de Geometría, Trigonometría y Física General (conocimientos adquiridos en el bachillerato), los cuales supondré que están bien entendidos por cada uno de mis Steemians-Lectores, por lo que no presentaré cálculos detallados.
Bien mis atentos Steemians-Lectores, presentaré un conjunto de sistemas mecánicos sencillos y analizaré las condiciones en las que se realizan los movimientos involucrados en cada uno de ellos. Al final, lo anterior, me permitirá definir Ligadura de forma muy clara y sencilla. |
|---|
SISTEMA 1
EL PENDULO SIMPLE: observemos, mis atentos Steemians-Lectores, el péndulo simple que les muestro en la figura 2. Aquí una partícula masa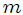 
(masa pendular) cuelga de un soporte mediante una cuerda de longitud 
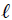, masa y elasticidad despreciable, en un campo gravitacional de intensidad 
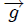, ocurriendo todo el movimiento en el plano 
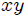. La partícula es ubicada usando un sistema de coordenadas Cartesianas, cuyo origen 
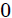se ha colocado en el punto de soporte.
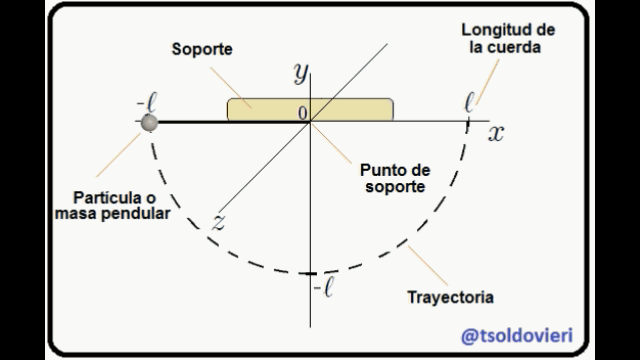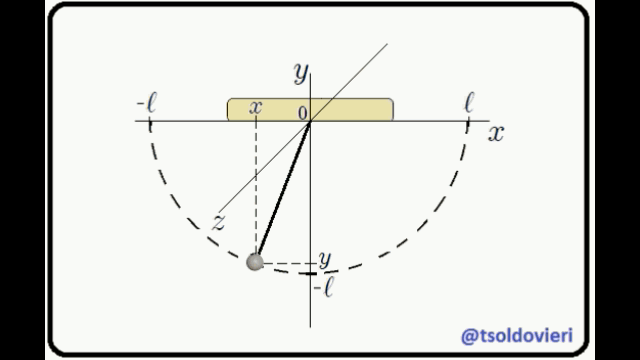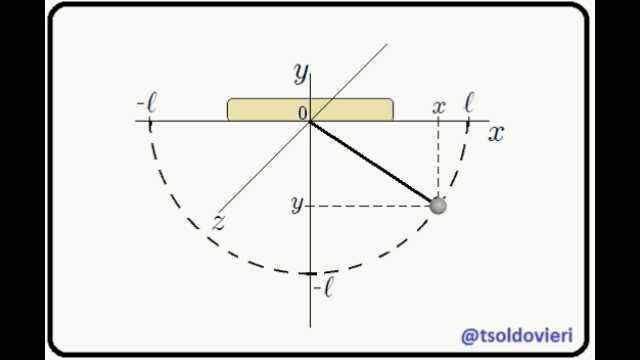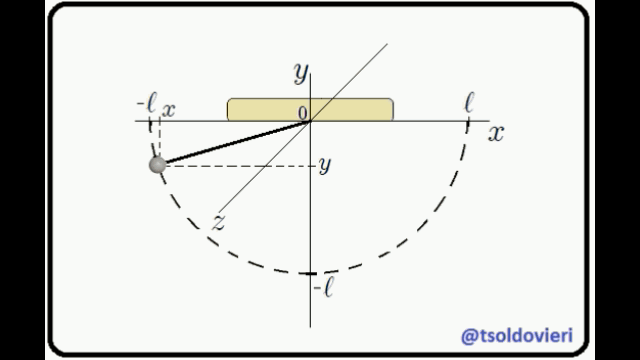
Ahora bien mis Steemians-Lectores, una partícula que es completamente libre puede moverse sin condicionamientos en todo el espacio sin problema alguno. Por el contrario, la partícula del péndulo no puede realizar un movimiento cualquiera pues debe hacerlo en el plano 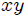, de tal forma que su distancia al punto de soporte 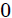sea constante e igual a 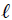. Es decir, el movimiento está condicionado. Las anteriores condiciones pueden ser expresadas matemáticamente como,
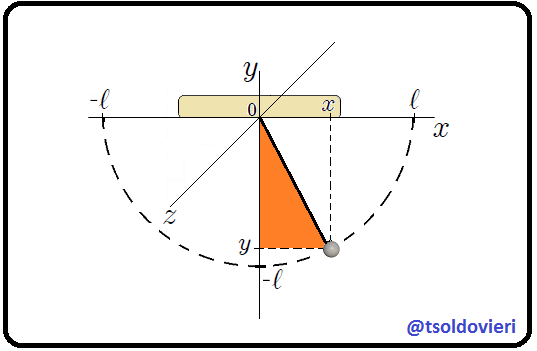
La primera condición es obvia. La segunda se obtiene al aplicar el Teorema de Pitágoras al triángulo rectángulo mostrado en la figura 3 (o a cualquiera de los triángulos que forma la cuerda con el eje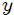 
).
SISTEMA 2
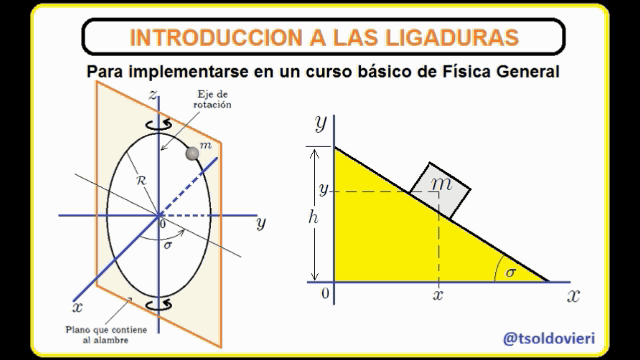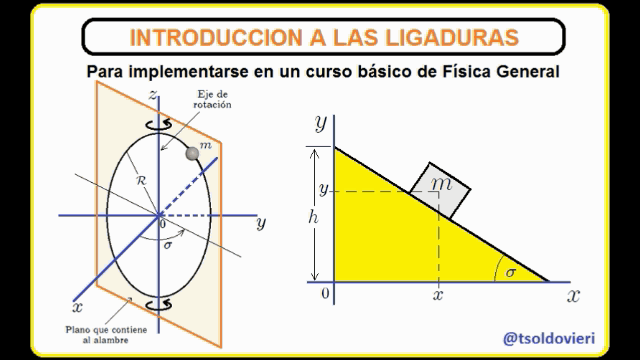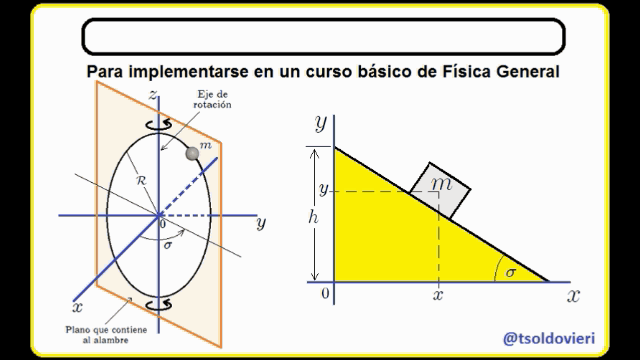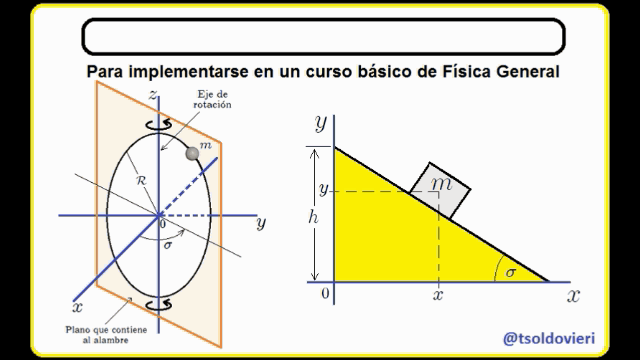
EL PLANO INCLINADO: observemos ahora, mis estimados Steemians-Lectores, el sistema mecánico que les muestro en la figura 4. Este es el caso típico de un bloque de masa 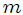que se mueve en el plano 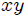, deslizándose sobre un plano inclinado.
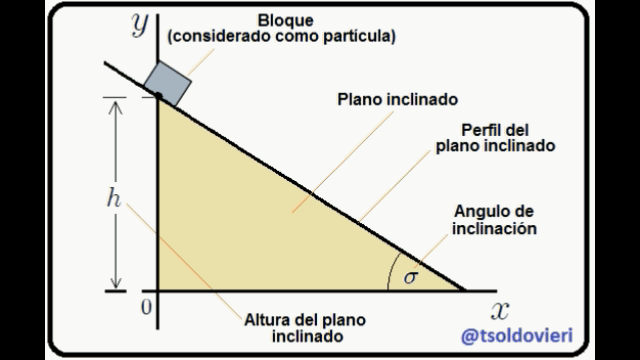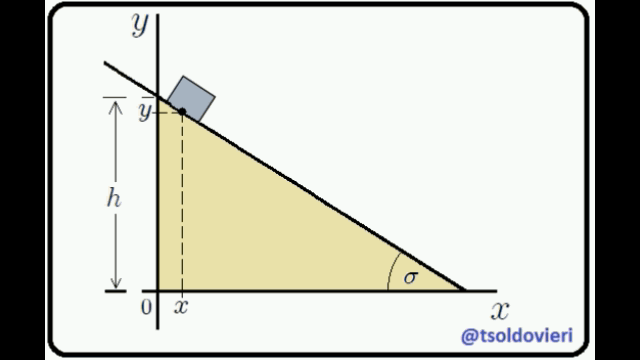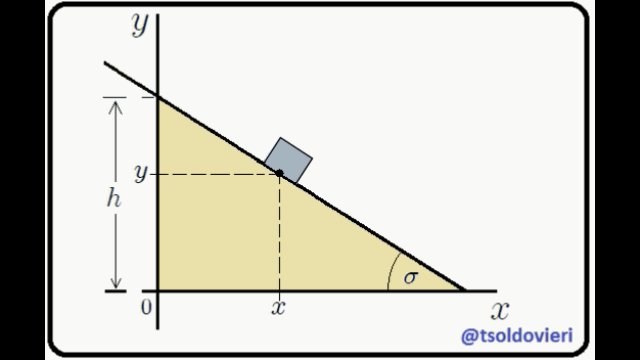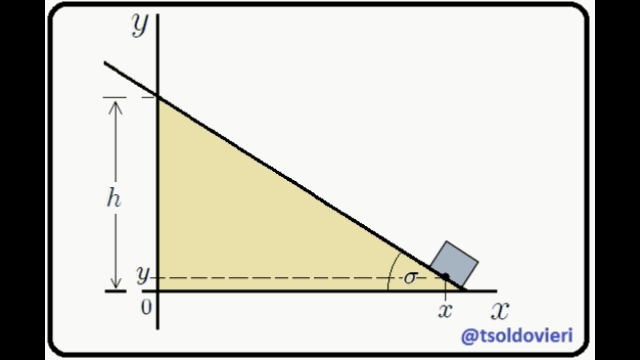
El bloque está condicionado a moverse sólo en el plano 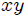y sobre el plano inclinado. Estas condiciones pueden ser expresadas matemáticamente mediante,
La primera condición es obvia. La segunda se obtiene al encontrar la ecuación de la recta que contiene el perfil del plano inclinado, lo cual es realmente sencillo de hacer.
SISTEMA 3
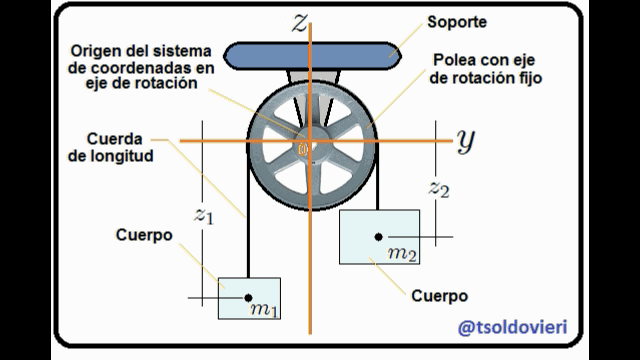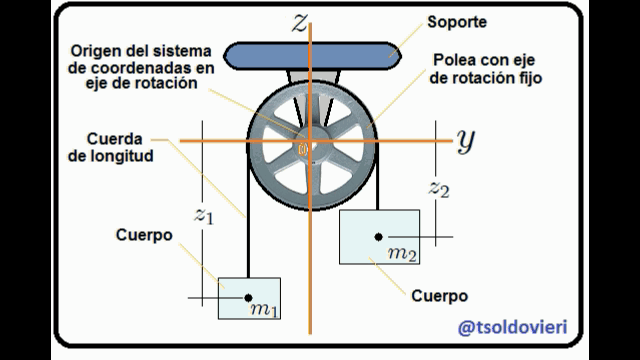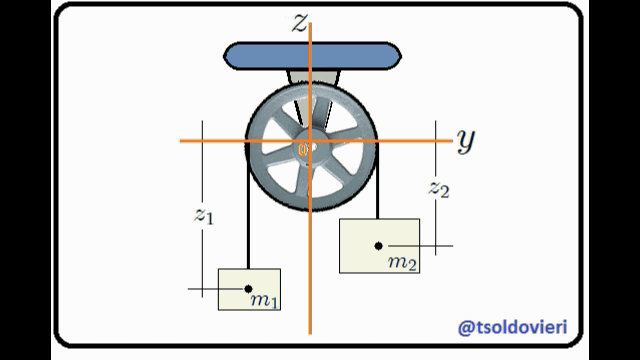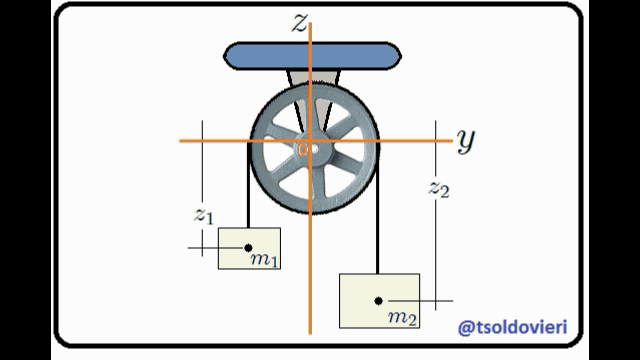
LA MAQUINA DE ATWOOD SIMPLE: una máquina de Atwood, mis Steemians-Lectores, es un dispositivo simple compuesto por una polea (fija en su centro) por la que pasa una cuerda, de cuyos extremos penden dos cuerpos de masas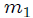 
y 
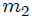. En el caso ideal, la deformación de la cuerda (elasticidad) y su masa, el tamaño de la polea y su masa, y toda posible fricción en el sistema son completamente despreciables. En la figura 5, mis Steemians-Lectores, les muestro un esquema de una máquina de este tipo, donde todo el movimiento se realiza en el plano 
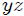y los cuerpos son posicionados mediante el uso de un sistema de coordenadas Cartesianas, cuyo origen coincide con la posición del eje de rotación de la polea.
Esta máquina fue inventada en 1784 por el Físico y Matemático inglés George Atwood 1745 - 1807 (ver figura 6), como un experimento de laboratorio para verificar las leyes mecánicas del movimiento uniformemente acelerado.
El movimiento de los cuerpos 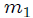y 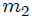está condicionado a que se lleve a cabo sólo en el plano 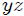. Adicionalmente a lo anterior se tiene que, debido a que el tamaño de la polea es despreciable, entonces ordenadas de la posición de cada cuerpo es nula, haciendo que ambos se muevan únicamente a lo largo del eje 
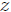. Además, debido a la cuerda, la separación entre los cuerpos se mantiene igual a la longitud 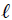de la misma. Matemáticamente estas condiciones se pueden expresar mediante,
Las condiciones 1 y 2 son obvias. En la condición 3 no se tomó en cuenta el trozo de cuerda que pasa sobre la polea puesto que su longitud es despreciable, por ser el tamaño de la polea igualmente despreciable.
SISTEMA 4
ESFERITA PERFORADA QUE SE DESLIZA A TRAVES DE UN ALAMBRE ROTANTE RECTO Y LISO: mis Steemians-Lectores, en la figura 7 les muestro una esferita, de masa 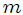y tamaño despreciable, perforada a través de su diámetro y que puede deslizarse a través de un alambre recto y liso (de masa despreciable) que pasa por su perforación, mientas que éste rota con velocidad angular constante 
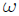. Todo el movimiento se realiza en el plano 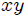. He utilizado un sistema coordenadas Cartesianas para ubicar la esferita, con origen posicionado en el eje de rotación del alambre.
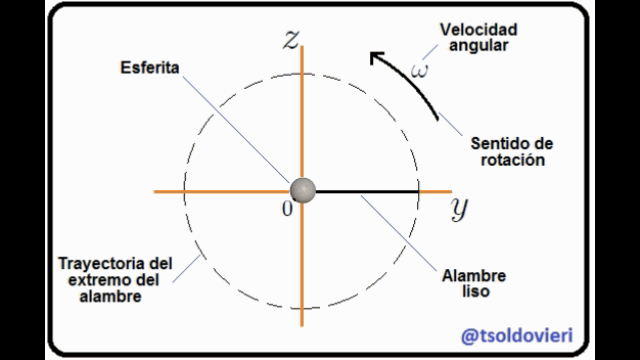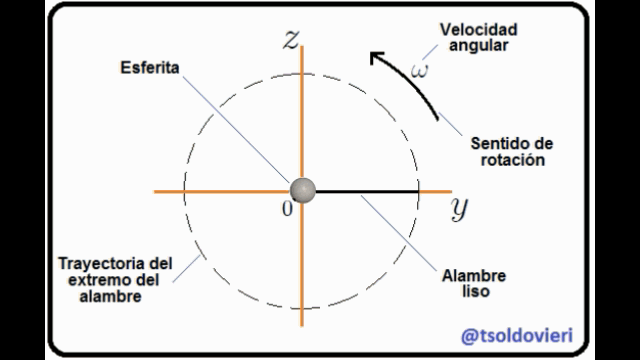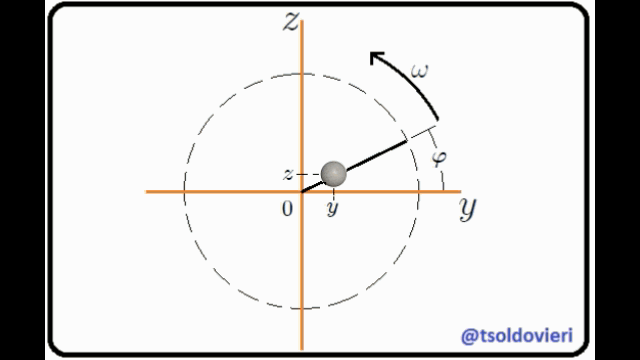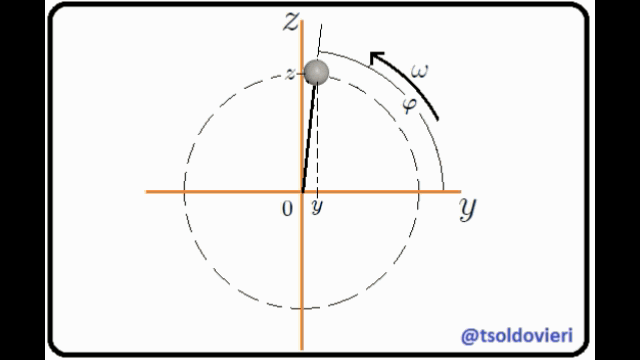
El movimiento de la esferita está condicionado a que sea en el plano 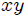y a lo largo del alambre liso. Matemáticamente estas condiciones se pueden expresar mediante,
La condición 1 es obvia. La condición 2 viene de la ecuación de la recta que contiene al alambre.
SISTEMA 5
ESFERITA PERFORADA QUE SE DESLIZA A TRAVES DE UN ARO LISO ROTANTE: continuando con la presentación de sistemas mecánicos, ahora les muestro en la figura 8 un sistema formado por una esferita de radio despreciable y de masa 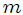que se desliza por un aro liso de radio 
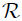y de masa despreciable, que pasa a través de un orificio en la misma. El aro gira con velocidad angular 
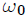constante de manera tal que el eje de rotación pasa a través de su diámetro. En esta oportunidad, mis atentos Steemians-Lectores, he posicionado la esferita usando un sistema de coordenadas Cartesianas y un sistema de coordenadas esféricas, ambos con origen posicionado en el centro del aro.
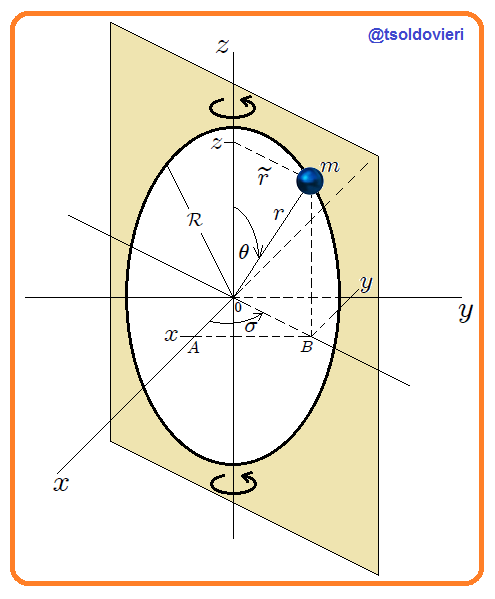
El movimiento de la esferita está condicionado a que sea a lo largo del aro y a que esté en rotación en conjunto con el mismo. Matemáticamente, en coordenadas Cartesianas, estas condiciones se pueden expresar mediante,
Las condiciones 1 y 2 se obtienen mediante simples consideraciones geométricas y trigonométricas.
En coordenadas cilíndricas y esféricas, las anteriores condiciones se pueden escribir como,
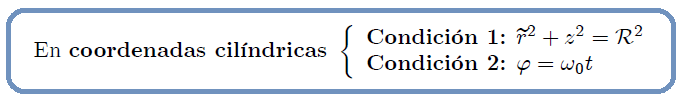
Para el caso de la coordenada radial de las coordenadas cilíndricas usé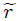 
para distinguirla de la coordenada radial 
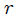de las coordenadas esféricas.
SISTEMA 6
MOLECULAS DE GAS ENCERRADAS EN UNA ESFERA: en la figura 9 les muestro, atentos Steemians-Lectores, un sistema de moléculas de gas encerrado en una esfera de radio 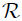. He utilizado coordenadas Cartesianas, centradas en el centro de la esfera, para la ubicación de las moléculas. Los vectores 
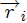son los vectores de posición (de módulos 
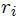) de cada una de las moléculas y 
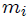sus masas, siendo 
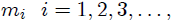hasta el número total de moléculas del sistema.
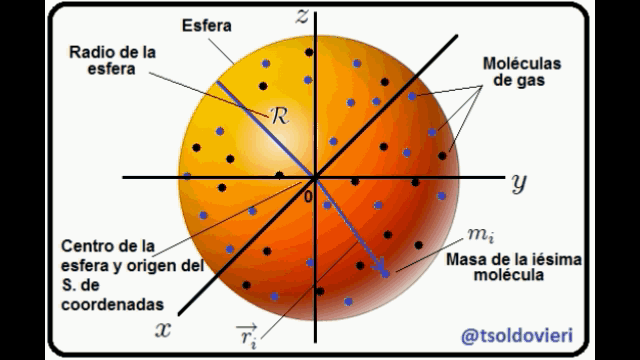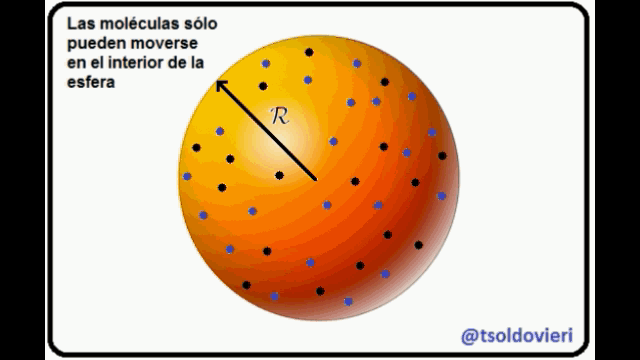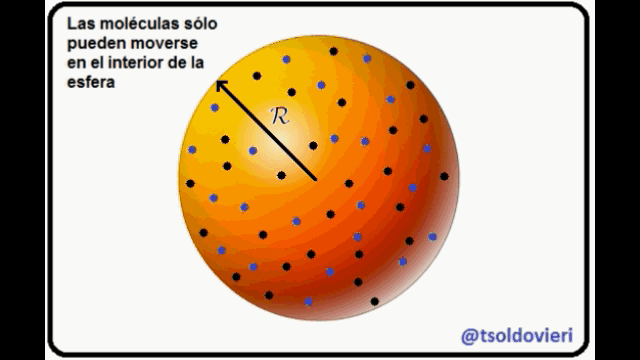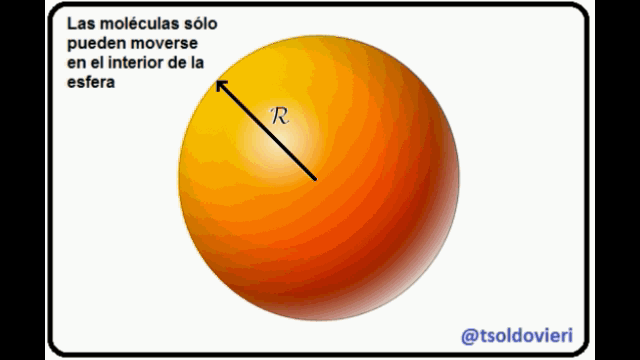
Cada una de las moléculas está condicionada a moverse dentro de la esfera o sobre su superficie interna, no pudiendo salir al exterior de la misma. La anterior condición que se aplica a cada una de las moléculas puede ser escrita matemáticamente como,
SISTEMA 7
PARTICULA QUE SE DESLIZA SOBRE LA SUPERFICIE DE UNA ESFERA LISA: ahora, mis muy estimados Steemians-Lectores, en la figura 10 les muestro un sistema mecánico que consta de una partícula de masa 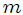que se desliza sobre la superficie de una esfera lisa de radio 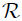. He utilizado, como en el sistema anterior, coordenadas Cartesianas centradas en el centro de la esfera para la ubicación de la partícula. El vector 
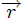es el vector de posición de la partícula y 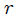su módulo.
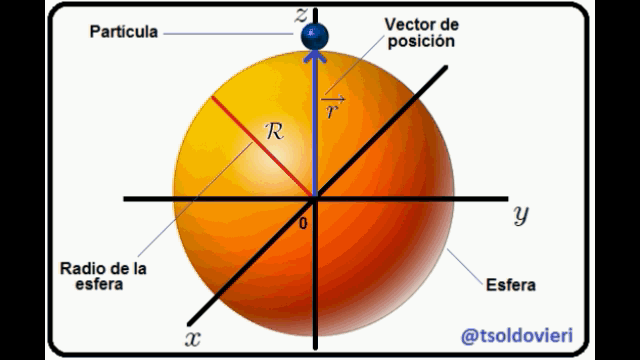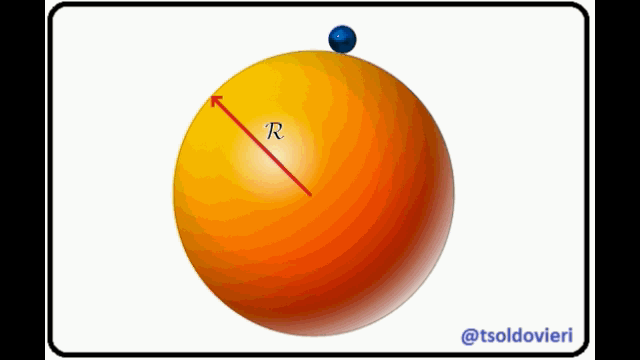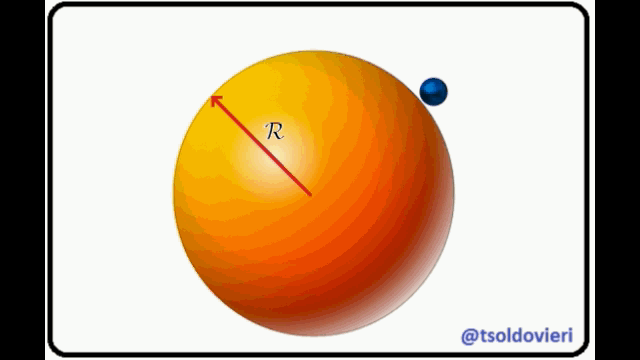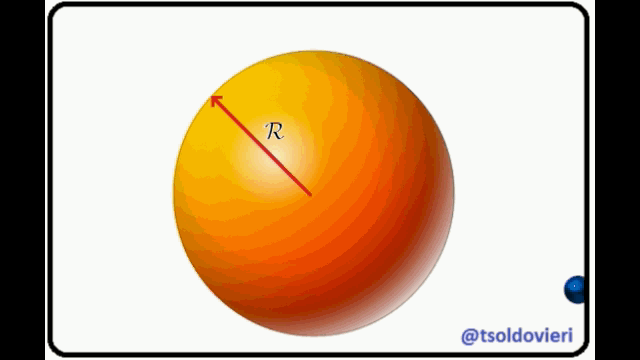
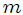que se desliza sobre la superficie de una esfera lisa (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).La partícula está condicionada a moverse sobre la superficie de la esfera o más allá de ella, pero nunca en su interior. La anterior condición puede ser escrita matemáticamente como,
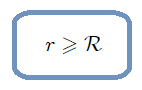
SISTEMA 8
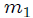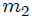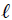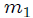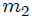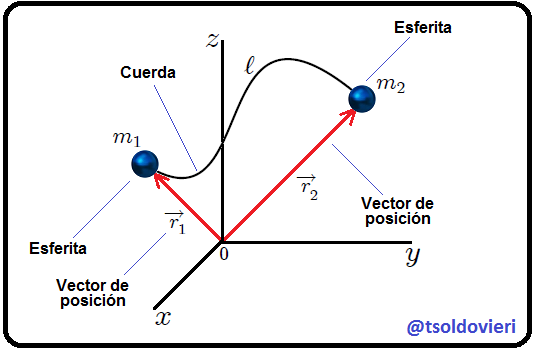
DOS ESFERITAS DE MASAS Y UNIDAS POR UNA CUERDA DE LONGITUD : finalmente, mis curiosos y atentos Steemians-Lectores, en la figura 11 les muestro un sistema mecánico que consta de dos esferitas de masas y unidas por una cuerda de longitud 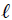de masa y elasticidad despreciables. Para ubicar las esferitas utilizo coordenadas Cartesianas, centradas en el centro de la esfera. Aquí 
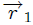y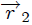 
son los vectores de posición de cada una de las esferitas, mientras que 
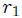y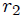 
son sus respectivos módulos.
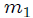y 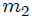unidas por una cuerda de longitud 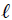, con masa y elasticidad despreciables (Figura realizada por mi persona @tsoldovieri, usando las aplicaciones PAINT y WORD).El movimiento de las esferitas está siempre condicionado a que la separación entre ellas no sea mayor que la longitud de la cuerda que las une. Matemáticamente, en coordenadas Cartesianas, estas condiciones se pueden expresar mediante,
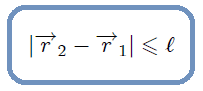
DISCUSION Y OBSERVACIONES
En los anteriores ejemplos, mis estimados Steemians-Lectores, les he presentado algunos ejemplos de sistemas mecánicos en los que me he concentrado, muy específicamente, en las limitaciones existentes en el movimiento de la partícula o partículas que los integran. Nos hemos podido dar cuenta, además, que esas limitaciones o condiciones pueden ser expresadas matemáticamente. Bien, a todas estos condicionamientos en el movimiento constituyen las denominadas Ligaduras, por lo tanto,
Se denominan Ligaduras a las condiciones que restringen la variedad de movimientos posibles de una partícula o de las partículas que constituyen un sistema de partículas. |
|---|
A las ecuaciones matemáticas que expresan las ligaduras se les denomina Ecuaciones de Ligadura, las cuales pueden ser igualdades o desigualdades. Pudimos notar también, mis atentos Steemians-Lectores que estas ecuaciones constituyen relaciones entre las coordenadas de la partícula o partículas que constituyen el sistema mecánico estudiado.
Otro detalle que pudimos notar es que algunas de las ecuaciones de ligadura no aparece el tiempo explícitamente, mientra que en otras sí. A las ligaduras del primer caso se les denomina Ligaduras Esclerónomas y a las del segundo caso se les denomina Ligaduras Reónomas. Las ligaduras esclerónomas no cambian al transcurrir el tiempo mientras que las reónomas si lo hacen, por lo que suelen denominarse también como Ligaduras Cinemáticas. Las ligaduras expresadas por las ecuaciones 1 a 3 y 8 a 10 son esclerónomas, y las expresadas por 4 y 5 son reónomas.
Las ligaduras que representan relaciones de igualdad sólo entre coordenadas se les denominan Ligaduras Holónomas y todas aquellas que no, se les denominan Ligaduras No-Holónomas. Las ligaduras expresadas por las ecuaciones 1 a 7 son holónomas y las expresadas por las ecuaciones 8 a 10 son no-holónomas (para ser holónomas tienen que ser igualdades y al mismo tiempo relaciones sólo entre coordenadas y estas ligaduras no cumplen con lo primero).
En realidad pueden existir ligaduras, expresadas por igualdades o desigualdades, que involucren velocidades, aceleraciones y otras variables. Estos casos no los traté aquí debido a que se necesitan matemáticas más avanzadas que el nivel aquí considerado. Todas estas ligaduras son no-holónomas a menos que puedan ser convertidas en igualdades entre coordenadas, pasando a ser así holónomas (por lo general esto ocurre en aquellas igualdades que puedan ser integradas, a las cuales suelen denominárseles Ligaduras Semi-Holónomas).
BIBLIOGRAFIA CONSULTADA Y RECOMENDADA
Para la elaboración del este post consulté 21 textos universitarios de distintos niveles en el área, los cuales muestro en la siguiente lista indicando la página consultada:
Soldovieri C., T. INTRODUCCION A LA MECANICA CLASICA. Preprint, Venezuela, 1era edición, 2018. El preprint puede ser descargado de la página http://www.cmc.org.ve/tsweb. Página 282.
Soldovieri C., T. INTRODUCCION A LA MECANICA DE LAGRAGE Y HAMILTON. Preprint, Venezuela, 1era edición, 2018. El preprint puede ser descargado de la página http://www.cmc.org.ve/tsweb. Página 67.
Chow, T. L. CLASSICAL MECHANICS. CRC Press - Taylor & Francis Group, LLC, 2nd edition, 2013. Página 85.
Dreizler, R. M. & Lüdde, C. S. THEORETICAL MECHANICS - THEORETICAL PHYSICS 1, volume 1 of Graduate Texts in Physics. Springer-Verlag Berlin Heidelberg, 1st edition, 2011. Página 186.
Strauch, D. CLASSICAL MECHANICS - AN INTRODUCTION. Springer-Verlag Berlin Heidelberg, 2009. Página 56.
Finn, J. M. CLASSICAL MECHANICS. Infinity Science Press LLC., 2008. Página 105.
Mahecha G., J. MECANICA CLASICA AVANZADA. Editorial Universidad de Antioquia, Colombia, 1era edición, 2006. Páginas 1 y 7.
Douglas G., R. CLASSICAL MECHANICS. Cambridge University Press, 2006. Página 323.
Ardema, M. D. ANALYTICAL DYNAMICS. Kluwer Academic / Plenum Publishers, New York, 2005. Página 47.
Fowles, G. R. & Cassiday, G. L. ANALYTICAL MECHANICS. Holt, Rinehard and Winston, 7th edition, 2005. Página 444.
Scheck, F. MECHANICS. Springer-Verlag, Berlin Heidelberg, 4th edition, 2005. Página 87.
Kibble, T. W. B. & Berkshire, F. H. CLASSICAL MECHANICS. Imperial College Press, London, 5th edition, 2004. Página 231.
Thornton, S. T. & Marion, J. B. CLASICAL DYNAMICS OF PARTICLES AND SYSTEMS. Thomson Brooks/Cole, 5th edition, 2004. Página 252.
Greiner, W. CLASSICAL MECHANICS SYSTEMS OF PARTICLES AND HAMILTONIAN DYNAMICS. Springer-Verlag New York, Inc., 2003. Página 314.
Fetter, A. L. & Walecka, J. D. THEORETICAL MECHANICS OF PARTICLES AND CONTINUA. Dover Publicatios, INC., Mineola, New York, 2003. Página 49.
Goldstein, H.; Poole, Ch. & Safko, J. CLASSICAL MECHANICS. Addison-Wesley, 3rd edition, 2000. Página 12.
Török, J. S. ANALYTICAL MECHANICS - WITH AN INTRODUCTION TO DYNAMICAL SYSTEMS. John Wiley & Sons, Inc., 2000. Página 94.
Baruh, H. ANALYTICAL DYNAMICS. McGraw-Hill, 1998. Página 219.
Calkin, M. G. LAGRANGIAN AND HAMILTONIAN MECHANICS. World Scientific Publishing Co. Pte. Ltd., 1998. Página 28.
José. J. V. & Saletan, E. J. CLASSICAL DYNAMICS - A CONTEMPORARY APPROACH. Cambridge University Press, 1998. Página 48.
Ruggieri C., G. MECANICA. Universidad Nacional Abierta (UNA), Caracas - Venezuela, 1994.
Con la anterior presentación, mis muy atentos y estimados Steemians-Lectores, introduje la Definición de Ligadura utilizada en los cursos avanzados de Mecánica Clásica, pero con un nivel adecuado para un curso de Física General 1. La ventaja de este tipo de presentación es que el estudiante irá a su curso avanzado de Mecánica Clásica con una preparación previa, lo cual debería traducirse en un mejor rendimiento en el entendimiento de los contenidos del curso avanzado.
Espero, como siempre, que la anterior información les sea de mucha utilidad, quedándoles claro así la definición de Ligadura y cómo esta puede implementarse a nivel de un curso de Física General 1. Si tienen preguntas no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta mi próximo post ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite las etiquetas #steemstem y #stem-espanol. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete a los canales de @steemstem y @stem-espanol. También puedes visitar el blog @steemstem y @stem-espanol para obtener mas información.
¡Felicitaciones!
Estas participando para optar a la mención especial, que se efectuará el 08 de Julio del 2018 a las 8:00 pm (hora de Venezuela); donde el autor del artículo seleccionado recibirá la cantidad de 1 SBD transferidos a su cuenta.
Contáctanos en Discord: https://discord.gg/hkCjFeb
Apoya al trail de entropía y así podrás ganar recompensas de curación de forma automática, entra aquí para más información sobre nuestro TRAIL.
Puedes consultar el reporte diario de curación visitando @entropia
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias @entropia por considerar a mi artículo como participante a la mención especial. Un cordial saludo.
Maestro @tsoldovieri encantado con tu explicación. Este concepto lo he utilizado al modelar estructuras en programas de cómputo, donde es necesario muchas veces, establecer la opción "constraints" en los nodos de la estructura, para de este modo, ajustar los grados de libertad de la estructura en cuestión, a sus condiciones de inercia y de rigidez. Excelente post maestro @tsoldovieri, muchos éxitos y saludos!!
Muchísimas gracias por tu muy motivador comentario amigo @eliaschess333, siempre trabajando duro en pro del desarrollo de las comunidades #stem-espanol #steemstem . Gracias por tu apoyo. Si, la determinación de las ligaduras es realmente importante en la Física y las ciencias relacionadas. Me alegra que te haya gustado. Mis saludos cordiales.
Este post quedo de lujo. Saludos estimado Colega. Felicitaciones
Muchísimas gracias mi muy hermosa colega @emily61. Siempre tratando de mejorar. Saludos.
Saludos cordiales profesor. Excelente artículo, muy bien formateado y didacticamente organizado con ilustraciones animadas perfectamente creadas.
Sin sinceras felicitaciones
Muchas gracias @ulisesfl17 por tu comentario tan positivo acerca de mi escrito. Ya te estoy siguiendo, sígueme si es de tu agrado. Saludos cordiales para ti también.
Hola @tsoldovieri. Como siempre impecable en el tema del formato y del uso de las herramientas gráficas y de visualización... Con relación al contenido messssmo... este es uno de los aspectos de la Mecánica Clásica donde la gente le saca el cuerpo, ya que la fenomenología de la dinámica están escondidas en las condiciones matemáticas de las ligaduras... En ese sentido, ¿cómo entender una ligadura holómona sin ecuaciones?...
Un abrazo y éxitos...
Amiguísimo y colega @jfermin70. Muchísimas gracias por los constantes piropos hacia mis publicaciones, las suyas están evolucionando muy pero muy bien en ese sentido también. Si, las ligaduras son muy importantes en la Mecánica Clásica. En ellas se esconden las llamadas Fuerzas de Ligadura, que son las encargadas de mantenerlas en acción. Como sabemos, es el empleo (en gran variedad de casos) de las ecuaciones que expresan a las ligaduras en las famosas Ecuaciones de movimiento de Lagrange y de Hamilton, lo que permite determinar las mencionadas fuerzas. Un fraterno abrazo.
Excelente profesor @tsoldovieri, como siempre una publicación muy didáctica y sencilla de entender. Felicitaciones por tan excelente trabajo.
Gracias amiga @ufv por tu comentario y apoyo. Saludos.
Excelente trabajo @tsoldovieri. Mejor explicado imposible. Las imágenes y tu didáctica son de primera. Mis felicitaciones. Saludos
Muchas gracias mi amigo y colega @lorenzor. Saludos.
Excelente @tsoldovieri. Las ligaduras y su muy santo profesor.
Amigo y colega @omar171, muchas gracias por tu comentario y apoyo. El Muy Santo Profesor 😈, le saluda cordialmente 😃
Saludos @tsoldovieri. Excelente post y muy didáctica la manera de introducir el concepto de ligadura, el cual es un dolor de cabeza en mecánica clásica.
Gracias por tu comentario y apoyo amigo @pparedes. Si, constituyen un verdadero dolor de cabeza en variedad de casos jajajajajaja
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thanks for the continuos support @steemstem. Always working hard to strengthen this community. Regards.
Hi @tsoldovieri!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks @utopian-io. Regards.
Buenísimo este post profesor, gracias por su valioso aporte a la comunidad. Saludos
Gracias por tu comentario y apoyo @arianadelg. Si, siempre ayudando a fortalecer la comunidad. Ya te estoy siguiendo, sígueme si es de tu agrado. Saludos.
gracias @tsoldovieri por publicar este post. La verdad es muy laborioso el trabajo. Explicar todo este tema es engorroso y tu lo logras con tus dibujos y graficos
Muchas gracias amigo y colega @germanmontero, por tu comentario y apoyo. Si, es de verdad laborioso. Consumo tiempo considerable elaborando esos gifs animados, pero vale la pena los resultados obtenidos. Un abrazo.
cada vez mas encantada de leerte, tu capacidad de enseñar traspasa las redes!
Es que soy un genio amiga @larissa22 ! Jajajajaja. Gracias por tu positivo comentario y apoyo!. Un abrazo.
Muy ilustrativo y cargado de buena información profesor @tsoldovieri, el tema de las ligaduras sin duda representa un reto en ocasiones, para una adecuada resolución de un fenómeno físico. Felicitaciones por su trabajo y saludos..!
Amigo @joseg, gracias por tu comentario y apoyo. Así es, frecuentemente representan un reto y es por esto que es mi pensar que deban ser introducidas, como tal, en los primeros cursos de Física en la carrera. En realidad algunas veces las utilizamos, sin saber que son ligaduras, en estos primeros cursos. Un saludo.